题目内容
某商场以每件30元的价格购进一种商品,试销中发现,这种商品每天的销售量m(件)与每件的销售价x(元)满足一次函数:m=162-3x.
(1)写出商场卖这种商品每天的销售利润y(元)与每件的销售价x(元)之间的函数关系式;
(2)若商场要想每天获得最大销售利润,每件商品的售价定为什么最合适?最大销售利润是多少?
(1)写出商场卖这种商品每天的销售利润y(元)与每件的销售价x(元)之间的函数关系式;
(2)若商场要想每天获得最大销售利润,每件商品的售价定为什么最合适?最大销售利润是多少?
(1)由题意得,每件商品的销售利润为(x-30)元,那么m件的销售利润为y=m(x-30),
又∵m=162-3x,
∴y=(x-30)(162-3x),
即y=-3x2+252x-4860,
∵x-30≥0,
∴x≥30.
又∵m≥0,
∴162-3x≥0,即x≤54.
∴30≤x≤54.
∴所求关系式为y=-3x2+252x-4860(30≤x≤54).
(2)由(1)得y=-3x2+252x-4860=-3(x-42)2+432,
所以可得售价定为42元时获得的利润最大,最大销售利润是432元.
又∵m=162-3x,
∴y=(x-30)(162-3x),
即y=-3x2+252x-4860,
∵x-30≥0,
∴x≥30.
又∵m≥0,
∴162-3x≥0,即x≤54.
∴30≤x≤54.
∴所求关系式为y=-3x2+252x-4860(30≤x≤54).
(2)由(1)得y=-3x2+252x-4860=-3(x-42)2+432,
所以可得售价定为42元时获得的利润最大,最大销售利润是432元.

练习册系列答案
相关题目




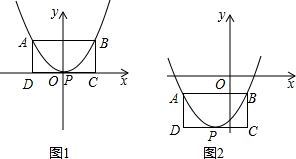 积为常数时,矩形ABCD需要满足什么条件并说明理由.
积为常数时,矩形ABCD需要满足什么条件并说明理由.
