题目内容
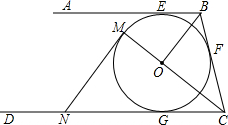 如图,AB、BC、CD分别与⊙O切于E、F、G,且AB∥CD.连接OB、OC,延长CO交⊙O于点M,过点M作MN∥OB交CD于N.
如图,AB、BC、CD分别与⊙O切于E、F、G,且AB∥CD.连接OB、OC,延长CO交⊙O于点M,过点M作MN∥OB交CD于N.(1)求证:MN是⊙O的切线;
(2)当0B=6cm,OC=8cm时,求⊙O的半径及MN的长.
分析:(1)求证:MN是⊙O的切线,就可以证明∠NMC=90°
(2)连接OF,则OF⊥BC,根据勾股定理就可以求出BC的长,然后根据△BOC的面积就可以求出⊙O的半径,根据△NMC∽△BOC就可以求出MN的长.
(2)连接OF,则OF⊥BC,根据勾股定理就可以求出BC的长,然后根据△BOC的面积就可以求出⊙O的半径,根据△NMC∽△BOC就可以求出MN的长.
解答:(1)证明:∵AB、BC、CD分别与⊙O切于点E、F、G
∴∠OBC=
∠ABC,∠DCB=2∠DCM(1分)
∵AB∥CD
∴∠ABC+∠DCB=180°
∴∠OBC+∠OCB=
(∠ABC+∠DCB)=
×180°=90°
∴∠BOC=180°-(∠OBC+∠OCB)=180°-90°=90°(2分)
∵MN∥OB
∴∠NMC=∠BOC=90°
即MN⊥MC 且MO是⊙O的半径
∴MN是⊙O的切线(4分)
(2)解:连接OF,则OF⊥BC(5分)
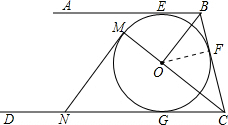 由(1)知,△BOC是直角三角形,
由(1)知,△BOC是直角三角形,
∴BC=
=
=10,
∵S△BOC=
•OB•OC=
•BC•OF
∴6×8=10×OF
∴0F=4.8cm
∴⊙O的半径为4.8cm(6分)
由(1)知,∠NCM=∠BCO,∠NMC=∠BOC=90°
∴△NMC∽△BOC(7分)
∴
=
,即
=
,
∴MN=9.6(cm).(8分)
∴∠OBC=
| 1 |
| 2 |
∵AB∥CD
∴∠ABC+∠DCB=180°
∴∠OBC+∠OCB=
| 1 |
| 2 |
| 1 |
| 2 |
∴∠BOC=180°-(∠OBC+∠OCB)=180°-90°=90°(2分)
∵MN∥OB
∴∠NMC=∠BOC=90°
即MN⊥MC 且MO是⊙O的半径
∴MN是⊙O的切线(4分)
(2)解:连接OF,则OF⊥BC(5分)
 由(1)知,△BOC是直角三角形,
由(1)知,△BOC是直角三角形,∴BC=
| OB2+OC2 |
| 62+82 |
∵S△BOC=
| 1 |
| 2 |
| 1 |
| 2 |
∴6×8=10×OF
∴0F=4.8cm
∴⊙O的半径为4.8cm(6分)
由(1)知,∠NCM=∠BCO,∠NMC=∠BOC=90°
∴△NMC∽△BOC(7分)
∴
| MN |
| OB |
| CM |
| CO |
| MN |
| 6 |
| 8+4.8 |
| 8 |
∴MN=9.6(cm).(8分)
点评:本题考查了切线的判定.要证某线是圆的切线,已知此线过圆上某点,连接圆心与这点(即为半径),再证垂直即可.

练习册系列答案
相关题目
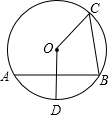 如图,AB,BC是⊙O的两条弦,AB垂直平分半径OD,∠ABC=75°,BC=
如图,AB,BC是⊙O的两条弦,AB垂直平分半径OD,∠ABC=75°,BC= 如图,AB,BC分别是⊙O的直径和弦,点D为
如图,AB,BC分别是⊙O的直径和弦,点D为
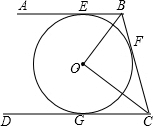 如图,AB,BC,CD分别与⊙O相切于E,F,G,且AB∥CD,BO=6cm,CO=8cm.求BC的长.
如图,AB,BC,CD分别与⊙O相切于E,F,G,且AB∥CD,BO=6cm,CO=8cm.求BC的长.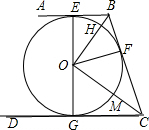 如图,AB、BC、CD分别与⊙O相切于E、F、G,且AB∥CD,BO=6,CO=8.
如图,AB、BC、CD分别与⊙O相切于E、F、G,且AB∥CD,BO=6,CO=8. 过点M作MN∥OB交CD于N,OB=6cm,OC=8cm.
过点M作MN∥OB交CD于N,OB=6cm,OC=8cm.