题目内容
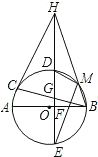 如图,AB,BC分别是⊙O的直径和弦,点D为
如图,AB,BC分别是⊙O的直径和弦,点D为 | BC |
求证:
(1)DE⊥AB;
(2)∠HMD=∠MHE+∠MEH.
分析:(1)连接OC,证明∠BFG=∠OCH=90°即可;
(2)连接BE,证明∠HMD=∠DEB=∠EMB即可.
(2)连接BE,证明∠HMD=∠DEB=∠EMB即可.
解答: 证明:(1)连接OC,
证明:(1)连接OC,
∵HC=HG,
∴∠HCG=∠HGC;(1分)
∵HC切⊙O于C点,
∴∠OCB+∠HCG=90°;(2分)
∵OB=OC,
∴∠OCB=∠OBC,(3分)
∵∠HGC=∠BGF,
∴∠OBC+∠BGF=90°,(4分)
∴∠BFG=90°,即DE⊥AB;(5分)
(2)连接BE,
由(1)知DE⊥AB,
∵AB是⊙O的直径,
∴
=
,(6分)
∴∠BED=∠BME;(7分)
∵四边形BMDE内接于⊙O,
∴∠HMD=∠BED,(8分)
∴∠HMD=∠BME;
∵∠BME是△HEM的外角,
∴∠BME=∠MHE+∠MEH,(9分)
∴∠HMD=∠MHE+∠MEH.(10分)
 证明:(1)连接OC,
证明:(1)连接OC,∵HC=HG,
∴∠HCG=∠HGC;(1分)
∵HC切⊙O于C点,
∴∠OCB+∠HCG=90°;(2分)
∵OB=OC,
∴∠OCB=∠OBC,(3分)
∵∠HGC=∠BGF,
∴∠OBC+∠BGF=90°,(4分)
∴∠BFG=90°,即DE⊥AB;(5分)
(2)连接BE,
由(1)知DE⊥AB,
∵AB是⊙O的直径,
∴
 |
| BD |
 |
| BE |
∴∠BED=∠BME;(7分)
∵四边形BMDE内接于⊙O,
∴∠HMD=∠BED,(8分)
∴∠HMD=∠BME;
∵∠BME是△HEM的外角,
∴∠BME=∠MHE+∠MEH,(9分)
∴∠HMD=∠MHE+∠MEH.(10分)
点评:此题综合性较强,主要考查了切线的性质、三角形的内角和外角的性质、等腰三角形的性质、内接四边形的性质.

练习册系列答案
相关题目
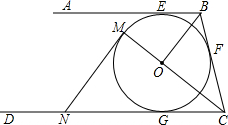 如图,AB、BC、CD分别与⊙O切于E、F、G,且AB∥CD.连接OB、OC,延长CO交⊙O于点M,过点M作MN∥OB交CD于N.
如图,AB、BC、CD分别与⊙O切于E、F、G,且AB∥CD.连接OB、OC,延长CO交⊙O于点M,过点M作MN∥OB交CD于N.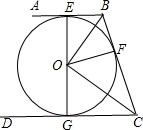 细心解一解
细心解一解 (2012•武汉模拟)如图,AB,BC,CD分别与⊙O相切于点E,F,G,且AB∥CD.OB与EF相交于点M,OC与FG相交于点N,连接MN.
(2012•武汉模拟)如图,AB,BC,CD分别与⊙O相切于点E,F,G,且AB∥CD.OB与EF相交于点M,OC与FG相交于点N,连接MN. 如图,AB、AC分别为⊙O的内接正六边形、内接正方形的一边,BC是圆内接n边形的一边,则n等于( )
如图,AB、AC分别为⊙O的内接正六边形、内接正方形的一边,BC是圆内接n边形的一边,则n等于( )