题目内容
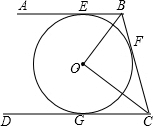 如图,AB,BC,CD分别与⊙O相切于E,F,G,且AB∥CD,BO=6cm,CO=8cm.求BC的长.
如图,AB,BC,CD分别与⊙O相切于E,F,G,且AB∥CD,BO=6cm,CO=8cm.求BC的长.
分析:根据切线长定理和平行线的性质定理得到△BOC是直角三角形.再根据勾股定理求出BC的长.
解答:解:∵AB,BC,CD分别与⊙O相切于E,F,G;
∴∠CBO=
∠ABC,∠BCO=
∠DCB,
∵AB∥CD,
∴∠ABC+∠DCB=180°,
∴∠CBO+∠BCO=
∠ABC+
∠DCB=
(∠ABC+∠DCB)=90°.
∴BC=
=
=10cm.
∴∠CBO=
| 1 |
| 2 |
| 1 |
| 2 |
∵AB∥CD,
∴∠ABC+∠DCB=180°,
∴∠CBO+∠BCO=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
∴BC=
| OB2+OC2 |
| 62+82 |
点评:解答此题的关键是综合运用切线长定理和平行线的性质发现Rt△BOC,再根据勾股定理进行计算.

练习册系列答案
相关题目
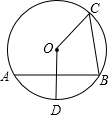 如图,AB,BC是⊙O的两条弦,AB垂直平分半径OD,∠ABC=75°,BC=
如图,AB,BC是⊙O的两条弦,AB垂直平分半径OD,∠ABC=75°,BC= 如图,AB,BC分别是⊙O的直径和弦,点D为
如图,AB,BC分别是⊙O的直径和弦,点D为
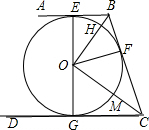 如图,AB、BC、CD分别与⊙O相切于E、F、G,且AB∥CD,BO=6,CO=8.
如图,AB、BC、CD分别与⊙O相切于E、F、G,且AB∥CD,BO=6,CO=8.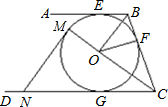 过点M作MN∥OB交CD于N,OB=6cm,OC=8cm.
过点M作MN∥OB交CD于N,OB=6cm,OC=8cm.