题目内容
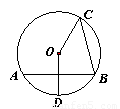
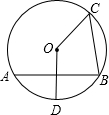 如图,AB,BC是⊙O的两条弦,AB垂直平分半径OD,∠ABC=75°,BC=4
如图,AB,BC是⊙O的两条弦,AB垂直平分半径OD,∠ABC=75°,BC=4| 2 |
分析:连接OA,OB.根据已知角度关系证明△BOC为等腰直角三角形求解.
解答: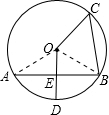 解:连接OA,OB.
解:连接OA,OB.
∵AB垂直平分半径OD,
∴OE=
OD=
OB,
∴∠OBE=30°,
又∵∠ABC=75°,
∴∠OBC=45°,
又∵OB=OC,
∴∠C=∠OBC=45°.
则△OBC是等腰直角三角形.
∴OC=
•BC=4cm.
 解:连接OA,OB.
解:连接OA,OB.∵AB垂直平分半径OD,
∴OE=
| 1 |
| 2 |
| 1 |
| 2 |
∴∠OBE=30°,
又∵∠ABC=75°,
∴∠OBC=45°,
又∵OB=OC,
∴∠C=∠OBC=45°.
则△OBC是等腰直角三角形.
∴OC=
| ||
| 2 |
点评:此题主要考查垂径定理、直角三角形的性质和勾股定理.

练习册系列答案
 世纪百通期末金卷系列答案
世纪百通期末金卷系列答案
相关题目
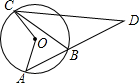 如图,AB、BC是⊙O的两条弦,延长AB到D点,连接BC使BD=BC.若∠AOC=100°,则∠D的度数为( )
如图,AB、BC是⊙O的两条弦,延长AB到D点,连接BC使BD=BC.若∠AOC=100°,则∠D的度数为( )| A、50° | B、45° | C、35° | D、25° |
 如图,AB与BC是两条笔直的公路,B与C是两个村庄.
如图,AB与BC是两条笔直的公路,B与C是两个村庄.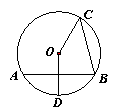
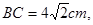 ,则OC的长为 ;
,则OC的长为 ;