题目内容
【题目】如图,四边形ABCD中,∠BAD=120°,∠B=∠D=90°,在BC、CD上分别找一点M、N,使△AMN周长最小时,则∠AMN+∠ANM的度数是 . 
【答案】120°
【解析】解:作A关于BC和CD的对称点A′,A″,连接A′A″,交BC于M,交CD于N,则A′A″即为△AMN的周长最小值.作DA延长线AH,
∵∠DAB=120°,
∴∠HAA′=60°,
∴∠AA′M+∠A″=∠HAA′=60°,
∵∠MA′A=∠MAA′,∠NAD=∠A″,
且∠MA′A+∠MAA′=∠AMN,∠NAD+∠A″=∠ANM,
∴∠AMN+∠ANM=∠MA′A+∠MAA′+∠NAD+∠A″=2(∠AA′M+∠A″)=2×60°=120°,
所以答案是:120°.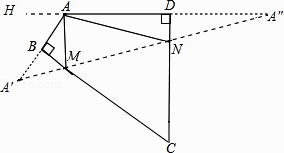
【考点精析】根据题目的已知条件,利用三角形的面积和三角形三边关系的相关知识可以得到问题的答案,需要掌握三角形的面积=1/2×底×高;三角形两边之和大于第三边;三角形两边之差小于第三边;不符合定理的三条线段,不能组成三角形的三边.

练习册系列答案
相关题目






