题目内容
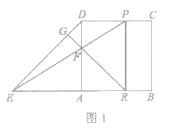
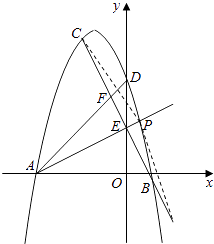
【题目】如图,已知△ABC的三个顶点坐标分别为A(﹣4,0)、B(1,0)、C(﹣2,6).
(1)求经过A、B、C三点的抛物线解析式;
(2)设直线BC交y轴于点E,连接AE,求证:AE=CE;
(3)设抛物线与y轴交于点D,连接AD交BC于点F,试问以A、B、F为顶点的三角形与△ABC相似吗?
(4)若点P为直线AE上一动点,当CP+DP取最小值时,求P点的坐标.
【答案】
(1)
解:设函数解析式为:y=ax2+bx+c,
由函数经过点A(﹣4,0)、B(1,0)、C(﹣2,6),
可得 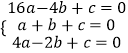 ,
,
解得: 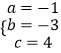 ,
,
故经过A、B、C三点的抛物线解析式为:y=﹣x2﹣3x+4
(2)
解:设直线BC的函数解析式为y=kx+b,
由题意得: ![]() ,
,
解得: ![]() ,
,
即直线BC的解析式为y=﹣2x+2.
故可得点E的坐标为(0,2),
从而可得:AE= ![]() =2
=2 ![]() ,CE=
,CE= ![]() =2
=2 ![]() ,
,
故可得出AE=CE
(3)
解:方法一:相似.理由如下:
设直线AD的解析式为y=kx+b,
则 ![]() ,
,
解得: ![]() ,
,
即直线AD的解析式为y=x+4.
联立直线AD与直线BC的函数解析式可得: ![]() ,
,
解得: 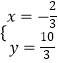 ,
,
即点F的坐标为(﹣ ![]() ,
, ![]() ),
),
则BF= ![]() =
= ![]() ,
,
又∵AB=5,BC= ![]() =3
=3 ![]() ,
,
∴ ![]() =
= ![]() ,
, ![]() =
= ![]() ,
,
∴ ![]() =
= ![]() ,
,
又∵∠ABF=∠CBA,
∴△ABF∽△CBA.
故以A、B、F为顶点的三角形与△ABC相似
方法二:
若△ABF∽△ABC,则 ![]() ,即AB2=BF×BC,
,即AB2=BF×BC,
∵A(﹣4,0),D(0,4),
∴lAD:y=x+4,lBC:y=﹣2x+2,
∴lAD与lBC的交点F(﹣ ![]() ,
, ![]() ),
),
∴AB=5,BF= ![]() ,BC=3
,BC=3 ![]() ,
,
∴AB2=25,BF×BC= ![]() ×3
×3 ![]() =25,
=25,
∴AB2=BF×BC,
又∵∠ABC=∠ABC,
∴△ABF∽△ABC
(4)
解:由(3)知:KAE= ![]() ,KCE=﹣2,
,KCE=﹣2,
∴KAE×KCE=﹣1,
∴AE⊥CE,
过C点作直线AE的对称点C‘,点E为CC′的中点,
∴ ![]() ,
, ![]() ,
,
∵C(﹣2,6),E(0,2),
∴C′X=2,C′Y=﹣2,
∵D(0,4),∴lC′D:y=﹣3x+4,
∵lAE:y= ![]() x+2,
x+2,
∴lC′D与lAE的交点P( ![]() ,
, ![]() )
)
【解析】(1)利用待定系数发求解即可得出抛物线的解析式;(2)求出直线BC的函数解析式,从而得出点E的坐标,然后分别求出AE及CE的长度即可证明出结论;(3)求出AD的函数解析式,然后结合直线BC的解析式可得出点F的坐标,由题意得∠ABF=∠CBA,然后判断出 ![]() 是否等于
是否等于 ![]() 即可作出判断.
即可作出判断.
【考点精析】根据题目的已知条件,利用二次函数的性质的相关知识可以得到问题的答案,需要掌握增减性:当a>0时,对称轴左边,y随x增大而减小;对称轴右边,y随x增大而增大;当a<0时,对称轴左边,y随x增大而增大;对称轴右边,y随x增大而减小.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案【题目】某校计划组织学生到市影剧院观看大型感恩歌舞剧,为了解学生如何去影剧院的问题,学校随机抽取部分学生进行调查,并将调查结果制成了表格、条形统计图和扇形统计图(均不完整). 
(1)此次共调查了多少位学生?
(2)将表格填充完整;
步行 | 骑自行车 | 坐公共汽车 | 其他 |
50 |
(3)将条形统计图补充完整.