题目内容
 已知如图,△ABC中,∠ACB=90°,AC=BC=
已知如图,△ABC中,∠ACB=90°,AC=BC=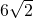 .
.
(1)四边形DEFG是△ABC内接正方形,求正方形DEFG的边长;
(2)点P从点B出发在线段BC上移动,PQ⊥AB于Q,以PQ为边在PQ的右侧作正方形PQMN,设PQ=x,正方形PQMN与△ABC公共面积为y,直接写出y与x之间的函数关系式.
 解:(1)如图,作CH⊥AB于H,交GF于T,则CH,CT分别是△ABC,△CGF的高线,
解:(1)如图,作CH⊥AB于H,交GF于T,则CH,CT分别是△ABC,△CGF的高线,∵四边形DEFG是正方形,
∴GF∥DE,
∴△CGF∽△ABC,
∴
 ,
,∵∠ACB=90°,AC=BC=
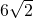 ,
,∴AB=12,CH=6,
设正方形DEFG的边长为a,则
 ,
,∴a=4,
故正方形DEFG的边长为4.
(2)
 .
.分析:(1)作出△ABC的高,利用正方形的性质与相似三角形的性质解决问题;
(2)分两种情况当正方形PQMN的边长不大于4时,即为△ABC内接正方形;当正方形PQMN的边长大于4不小于6时,即可解决问题.
点评:此题主要考查正方形的性质,正方形的面积,以及相似三角形的判定与性质.

练习册系列答案
相关题目
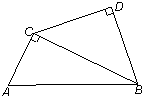 已知如图,△ABC中,∠ACB=90°,△BCD中,∠D=90°,CD=BD,又AC=6,tan∠ABC=
已知如图,△ABC中,∠ACB=90°,△BCD中,∠D=90°,CD=BD,又AC=6,tan∠ABC= 7、已知如图,△ABC中,D在BC上,且∠1=∠2,请你在空白处填一个适当的条件:当
7、已知如图,△ABC中,D在BC上,且∠1=∠2,请你在空白处填一个适当的条件:当 已知如图,△ABC中,BD⊥AC于D,tanA=
已知如图,△ABC中,BD⊥AC于D,tanA=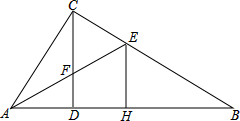 已知如图在△ABC中,∠ACB=90°,CD⊥AB于D,∠A的平分线交CD于F,BC于E,过点E作EH⊥AB于H.求证:EC=CF=EH.
已知如图在△ABC中,∠ACB=90°,CD⊥AB于D,∠A的平分线交CD于F,BC于E,过点E作EH⊥AB于H.求证:EC=CF=EH.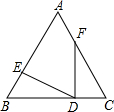 已知如图:△ABC中,AB=AC,BE=CD,BD=CF,则∠EDF=( )
已知如图:△ABC中,AB=AC,BE=CD,BD=CF,则∠EDF=( )