题目内容
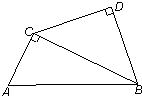 已知如图,△ABC中,∠ACB=90°,△BCD中,∠D=90°,CD=BD,又AC=6,tan∠ABC=
已知如图,△ABC中,∠ACB=90°,△BCD中,∠D=90°,CD=BD,又AC=6,tan∠ABC=| 1 | 2 |
分析:首先由,△ABC中,∠ACB=90°,AC=6,tan∠ABC=
,求出BC,又由,△BCD中,∠D=90°,CD=BD,可求出BD、CD,从而求出△BCD的面积.
| 1 |
| 2 |
解答:解:在Rt△ABC中,tan∠ABC=
=
(1分)
∵AC=6
∴BC=12(2分)
在Rt△BCD中,由勾股定理得:CD2+BD2=BC2
∵CD=BD,则有2CD2=144
解得CD=6
(舍负)
∴BD=CD=6
(4分)
∴S△BCD=
BD•CD=36(5分)
| AC |
| BC |
| 1 |
| 2 |
∵AC=6
∴BC=12(2分)
在Rt△BCD中,由勾股定理得:CD2+BD2=BC2
∵CD=BD,则有2CD2=144
解得CD=6
| 2 |
∴BD=CD=6
| 2 |
∴S△BCD=
| 1 |
| 2 |
点评:本题考查的知识点是勾股定理与锐角三角函数的定义,解题的关键是由函数值先求出BC,再根据勾股定理求出BD、CD.

练习册系列答案
 口算题卡北京妇女儿童出版社系列答案
口算题卡北京妇女儿童出版社系列答案
相关题目
 7、已知如图,△ABC中,D在BC上,且∠1=∠2,请你在空白处填一个适当的条件:当
7、已知如图,△ABC中,D在BC上,且∠1=∠2,请你在空白处填一个适当的条件:当 已知如图,△ABC中,BD⊥AC于D,tanA=
已知如图,△ABC中,BD⊥AC于D,tanA= 已知如图在△ABC中,∠ACB=90°,CD⊥AB于D,∠A的平分线交CD于F,BC于E,过点E作EH⊥AB于H.求证:EC=CF=EH.
已知如图在△ABC中,∠ACB=90°,CD⊥AB于D,∠A的平分线交CD于F,BC于E,过点E作EH⊥AB于H.求证:EC=CF=EH.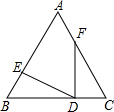 已知如图:△ABC中,AB=AC,BE=CD,BD=CF,则∠EDF=( )
已知如图:△ABC中,AB=AC,BE=CD,BD=CF,则∠EDF=( )