题目内容
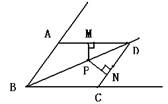
 已知如图在△ABC中,∠ACB=90°,CD⊥AB于D,∠A的平分线交CD于F,BC于E,过点E作EH⊥AB于H.求证:EC=CF=EH.
已知如图在△ABC中,∠ACB=90°,CD⊥AB于D,∠A的平分线交CD于F,BC于E,过点E作EH⊥AB于H.求证:EC=CF=EH.分析:先由已知证明△ACE≌△AHE,得∠AEC=∠AEH,再由CD⊥AB,EH⊥AB推出CD∥EH得∠HEF=∠CFE,所以得∠CEF=∠CFE,从而证得CF=CE.
解答:证明:∵AE平分∠CAB,∠ACB=90°,EH⊥AB,
∴EH=CE,
∵∠ACE=∠AHE=90°,
∴在Rt△ACE和Rt△AHE中
∴Rt△ACE≌Rt△AHE(HL)
∴∠AEC=∠AHG,
∵CD⊥AB,EG⊥AB
∴CD∥EH,
∴∠HEF=∠CFE,
∴∠CEF=∠CFE,
∴CF=CE,
即EC=CF=EH.
∴EH=CE,
∵∠ACE=∠AHE=90°,
∴在Rt△ACE和Rt△AHE中
|
∴Rt△ACE≌Rt△AHE(HL)
∴∠AEC=∠AHG,
∵CD⊥AB,EG⊥AB
∴CD∥EH,
∴∠HEF=∠CFE,
∴∠CEF=∠CFE,
∴CF=CE,
即EC=CF=EH.
点评:本题考查了等腰三角形的性质和判定,全等三角形的性质和判定,角平分线性质的应用,主要考查学生的推理能力.

练习册系列答案
 夺冠金卷全能练考系列答案
夺冠金卷全能练考系列答案
相关题目
 ,sin∠BCE=
,sin∠BCE= . 求CE的长.
. 求CE的长.
 ,sin∠BCE=
,sin∠BCE= . 求CE的长.
. 求CE的长.
 ,sin∠BCE=
,sin∠BCE= . 求CE的长.
. 求CE的长.
 AB=CB (已知)
AB=CB (已知)