题目内容
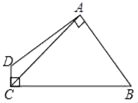
【题目】如图,Rt△ABC中,直角边AC=7cm,BC=3cm,CD为斜边AB上的高,点E从点B出发沿直线BC以2cm/s的速度移动,过点E作BC的垂线交直线CD于点F. 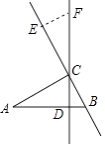
(1)求证:∠A=∠BCD;
(2)点E运动多长时间,CF=AB?并说明理由.
【答案】
(1)解:∵∠A+∠ACD=90°,∠BCD+∠ACD=90°,
∴∠A=∠BCD,
(2)解:如图,
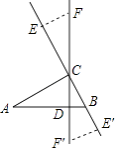
当点E在射线BC上移动时,若E移动5s,则BE=2×5=10cm,
∴CE=BE﹣BC=10﹣3=7cm.
∴CE=AC,
在△CFE与△ABC中  ,
,
∴△CEF≌△ABC,
∴CF=AB,
当点E在射线BC上移动时,若E移动2s,则BE′=2×2=4cm,
∴CE′=BE′+BC=4+3=7cm,
∴CE′=AC,
在△CF′E′与△ABC中 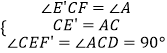 ,
,
∴△CF′E′≌△ABC,
∴CF′=AB,
总之,当点E在射线BC上移动5s,或2s时,CF′=AB.
【解析】(1)根据余角的性质即可得到结论;(2)如图,当点E在射线BC上移动时,若E移动5s,则BE=2×5=10cm,根据全等三角形的判定和性质即可得到结论.

练习册系列答案
相关题目