题目内容
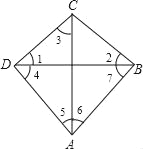
【题目】如图,BC⊥CD,∠1=∠2=∠3,∠4=60°,∠5=∠6.
(1)CO是△BCD的高吗?为什么?
(2)求∠5、∠7的度数.
【答案】(1)CO是△BCD的高.理由见解析;(2)60°.
【解析】
(1)由BC⊥CD,则∠DCB=90°,可得∠1=∠2=∠3=45°,即CD=CB,所以,CO是等腰直角△DCB的角平分线,则可得CO⊥BD;
(2)在△ACD中,由∠1=∠3=45°,∠4=60°,根据三角形的内角和定理,可求得∠5=30°,又∠5=∠6,所以,在直角△AOB中,即可得出∠7的度数;
(1)CO是△BCD的高.理由如下:
∵BC⊥CD,
∴∠DCB=90°,
∴∠1=∠2=∠3=45°,
∴△DCB是等腰直角三角形,
∴CO是∠DCB的角平分线,
∴CO⊥BD(等腰三角形三线合一);
(2)∵在△ACD中,∠1=∠3=45°,∠4=60°,
∴∠5=30°,
又∵∠5=∠6,
∴∠6=30°,
∴在直角△AOB中,
∠7=180°﹣90°﹣30°=60°.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目