题目内容
【题目】如图,在△ABC中,B、C两点恰好在反比例函数y= ![]() (k>0)第一象限的图象上,且BC=
(k>0)第一象限的图象上,且BC= ![]() ,S△ABC=
,S△ABC= ![]() ,AB∥x轴,CD⊥x轴交x轴于点D,作D关于直线BC的对称点D′.若四边形ABD′C为平行四边形,则k为 .
,AB∥x轴,CD⊥x轴交x轴于点D,作D关于直线BC的对称点D′.若四边形ABD′C为平行四边形,则k为 . 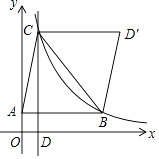
【答案】8
【解析】解:设AB交CD于H.
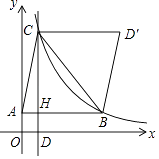
由题意AB=CD′=CD,
∴B、C两点关于直线y=x对称,设C(a,b),则B(b,a),
∵S△ABC= ![]() ,
,
∴ ![]() b(b﹣a)=
b(b﹣a)= ![]() ,∵ab=k,
,∵ab=k,
∴b=2 ![]() ,a=
,a= ![]() ,
,
∴CH=BH= ![]() ,
,
∵BC= ![]() ,
,
∴BC= ![]() BH,
BH,
∴ ![]() k=
k= ![]()
![]() ,
,
解得k=8.
所以答案是:8.
【考点精析】利用比例系数k的几何意义和平行四边形的性质对题目进行判断即可得到答案,需要熟知几何意义:表示反比例函数图像上的点向两坐标轴所作的垂线段与两坐标轴围成的矩形的面积;平行四边形的对边相等且平行;平行四边形的对角相等,邻角互补;平行四边形的对角线互相平分.

练习册系列答案
相关题目