题目内容
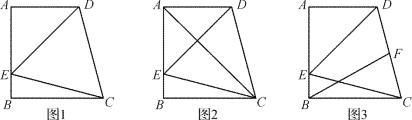
【题目】如图1所示,在四边形ABCD中,AD∥BC, AB⊥BC,∠DCB=75,以CD为一边的等边△DCE的另一顶点E在边AB上.
(1)求∠AED的度数;
(2)连接AC,如图2所示,试判断△ABC的形状;
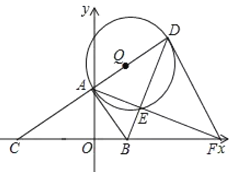
(3)如图3所示,若F为线段CD上一点,AB=4,∠FBC=30,求DF的长.
【答案】(1) 45°;(2)△ABC的形状是等腰直角三角形,理由见解析;(3) ![]()
【解析】
(1)根据直线平行的性质得到∠ADC的度数,再根据等边三角形的性质和AB⊥BC即可得到答案;
(2)先证A在线段DE的垂直平分线上,再证明点C也在线段DE的垂直平分线上,最后得到BA=BC,即可得到△ABC的形状;
(3) 连接AF,BF、AD的延长线交于点G,证△BCF≌△GDF(ASA)得到DF=CF,再根据三角函数值计算即可得到答案;
解:(1)∵∠DCB=75,AD∥BC,
∴∠ADC=180°-75°=105°(两直线平行,同旁内角互补),
又∵△DCE是等边三角形,
∴∠CDE=60°,
故∠ADE=105°-60°=45°,
又∵AD∥BC, AB⊥BC,
∴∠DAB=90°,
∴∠AED=180°-90°-45°=45°;
(2) 由(1)知∠AED=45°,
∴AD=AE,
故点A在线段DE的垂直平分线上,
又∵△DCE是等边三角形,
∴CD=CE,
故点C也在线段DE的垂直平分线上,
∴AC就是线段DE的垂直平分线,即AC⊥DE,
∵∠AED=45°,
∴∠BAC=45°,
又∵AB⊥BC,
∴BA=BC,
故△ABC的是等腰直角三角形;
(3) 连接AF,BF、AD的延长线交于点G,如下图:

∵∠FBC=30,∠DCB=75,
∴∠BFC=75°,
∴BC=BF,
又由(2)知BA=BC,
∴BF=BC(等量替换),
∴∠ABF=90°-30°=60°,
∴AB=BF=FA,
又∵AD∥BC, AB⊥BC,
∴∠FAG=∠G=30°,
∴FG=FA=FB,
∵∠G=∠FBC=30°,∠DFG=∠CFB,FB=FG,
∴△BCF≌△GDF(ASA),
∴DF=CF,
又∵根据题意得: ,
,
我们知道![]() ,
,
∴ ,
,
∴DF=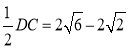 ;
;

 阅读快车系列答案
阅读快车系列答案【题目】在等腰直角三角形![]() 中,
中,![]() ,
,![]() .点
.点![]() 为射线
为射线![]() 上一个动点,连接
上一个动点,连接![]() ,点
,点![]() 在直线
在直线![]() 上,且
上,且![]() .过点
.过点![]() 作
作![]() 于点
于点![]() ,点
,点![]() ,
,![]() 在直线
在直线![]() 的同侧,且
的同侧,且![]() ,连接
,连接![]() .请用等式表示线段
.请用等式表示线段![]() ,
,![]() ,
,![]() 之间的数量关系.小明根据学习函数的经验.对线段
之间的数量关系.小明根据学习函数的经验.对线段![]() ,
,![]() ,
,![]() 的长度之间的关系进行了探究.下面是小明的探究过程,请补充完整:
的长度之间的关系进行了探究.下面是小明的探究过程,请补充完整:
(1)对于点![]() 在射线
在射线![]() 上的不同位置,画图、测量,得到了线段
上的不同位置,画图、测量,得到了线段![]() ,
,![]() ,
,![]() 的长度的几组值,如下表:
的长度的几组值,如下表:
位置 1 | 位置 2 | 位置 3 | 位置 4 | 位置 5 | 位置 6 | 位置 7 | 位置 8 | |
| 2.83 | 2.83 | 2.83 | 2.83 | 2.83 | 2.83 | 2.83 | 2.83 |
| 2.10 | 1.32 | 0.53 | 0.00 | 1.32 | 2.10 | 4.37 | 5.6 |
| 0.52 | 1.07 | 1.63 | 2.00 | 2.92 | 3.48 | 5.09 | 5.97 |
在![]() ,
,![]() ,
,![]() 的长度这三个量中,确定 的长度是自变量, 的长度是这个自变量的函数, 的长度是常量.
的长度这三个量中,确定 的长度是自变量, 的长度是这个自变量的函数, 的长度是常量.
(2)在同一平面直角坐标系![]() 中,画出(1)中所确定的函数的图象;
中,画出(1)中所确定的函数的图象;
(3)结合函数图象,解决问题:请用等式表示线段![]() ,
,![]() ,
,![]() 之间的数量关系.
之间的数量关系.