题目内容
【题目】已知二次函数![]() ,其中a>0.
,其中a>0.
(1)若方程![]() 有两个实根
有两个实根![]() ,且方程
,且方程![]() 有两个相等的实根,求二次函数的解析式;
有两个相等的实根,求二次函数的解析式;
(2)若二次函数![]() 的图象与x轴交于
的图象与x轴交于![]() 两点,且当
两点,且当![]() 时,
时,![]() 恒成立,求实数m的取值范围.
恒成立,求实数m的取值范围.
【答案】(1)二次函数的解析式为![]() ;(2)实数m的取值范围为
;(2)实数m的取值范围为![]() .
.
【解析】
(1)先分别根据一元二次方程的根的定义、根的判别式列出等式求出a、b、c的值,由此即可得出答案;
(2)先得出二次函数的表达式,再求出其对称轴,然后根据二次函数的增减性、对称轴分三种情况讨论,分别列出不等式(或不等式组)求解即可得.
(1)由题意得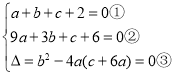
由②![]() ①得
①得![]() ,解得
,解得![]()
将![]() 代入①得
代入①得![]() ,解得
,解得![]()
将![]() ,
,![]() 代入③得
代入③得![]()
整理得![]()
解得![]() 或
或![]() (不符题意,舍去)
(不符题意,舍去)
则![]() ,
,![]()
故二次函数的解析式为![]() ;
;
(2)由题意得:![]() 是方程
是方程![]() 的两个根
的两个根
则![]() ,
,![]()
解得![]() ,
,![]()
因此,二次函数的解析式为![]()
此二次函数的对称轴为![]() ,开口方向向上;当
,开口方向向上;当![]() 时,y随x的增大而减小;当
时,y随x的增大而减小;当![]() 时,y随x增大而增大
时,y随x增大而增大
分以下三种情况:
①当![]() ,即
,即![]() 时
时
此时,在![]() 时,y随x的增大而减小
时,y随x的增大而减小
要使当![]() 时,
时,![]() 恒成立,则当
恒成立,则当![]() 时,y的值小于或等于0
时,y的值小于或等于0
即![]()
解得![]()
则![]()
②当![]() ,即
,即![]() 时
时
此时,在![]() 时,y随x的增大而减小;当
时,y随x的增大而减小;当![]() 时,y随x的增大而增大
时,y随x的增大而增大
要使当![]() 时,
时,![]() 恒成立,则当
恒成立,则当![]() 和
和![]() 时,y的值小于或等于0
时,y的值小于或等于0
即![]()
解得![]()
则![]()
③当![]() ,即
,即![]() 时
时
此时,在![]() 时,y随x的增大而增大
时,y随x的增大而增大
要使当![]() 时,
时,![]() 恒成立,则当
恒成立,则当![]() 时,y的值小于或等于0
时,y的值小于或等于0
即![]()
解得![]()
则![]()
综上,实数m的取值范围为![]() .
.

练习册系列答案
相关题目