题目内容
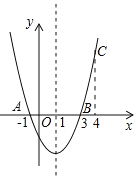
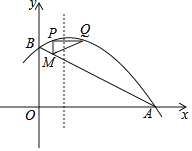
【题目】如图,在平面直角坐标系中,抛物线y=ax2+![]() x+2与x轴交于点A(4,0)与y轴交于点B.点M在线段AB上,其横坐标为m,PM∥y轴,与抛物线交点为点P,PQ∥x轴,与抛物线交点为点Q
x+2与x轴交于点A(4,0)与y轴交于点B.点M在线段AB上,其横坐标为m,PM∥y轴,与抛物线交点为点P,PQ∥x轴,与抛物线交点为点Q
(1)求a的值、并写出此抛物线顶点的坐标;
(2)求m为何值时,△PMQ为等腰直角三角形.
【答案】(1)a=﹣![]() ,y=﹣
,y=﹣![]() x2+
x2+![]() x+2,顶点(1,
x+2,顶点(1,![]() );(2)m=6﹣2
);(2)m=6﹣2![]() 或2
或2![]() ﹣2
﹣2
【解析】
(1)将A(4,0)代入抛物线y=ax2+![]() x+2求出a的值,然后将二次函数的一般式化为顶点式即可求出顶点坐标;
x+2求出a的值,然后将二次函数的一般式化为顶点式即可求出顶点坐标;
(2)先利用待定系数法求出直线AB的解析式,设P(m,﹣![]() m2+
m2+![]() m+2),M(m,
m+2),M(m,![]() m+2),从而求出PM,分两种情况讨论当0<m≤1时和当1<m<4时,分别利用二次函数的对称性用含m的式子表示出PQ,然后利用PM=PQ列方程即可求出m的值.
m+2),从而求出PM,分两种情况讨论当0<m≤1时和当1<m<4时,分别利用二次函数的对称性用含m的式子表示出PQ,然后利用PM=PQ列方程即可求出m的值.
解:(1)∵抛物线y=ax2+![]() x+2与x轴交于点A(4,0),
x+2与x轴交于点A(4,0),
∴16a+![]() ×4+2=0,
×4+2=0,
解得a=﹣![]() ,
,
∴此抛物线解析式y=﹣![]() x2+
x2+![]() x+2,
x+2,
化为顶点式y=﹣![]() (x-1)2+
(x-1)2+![]()
∴顶点坐标为(1,![]() ).
).
(2)∵y=﹣![]() x2+
x2+![]() x+2,
x+2,
∴B(0,2),
∵A(4,0),
设直线AB的解析式为y=kx+b
将A、B两点坐标代入,得
![]()
解得: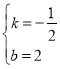
∴直线AB:y=![]() x+2,
x+2,
设P(m,﹣![]() m2+
m2+![]() m+2),M(m,
m+2),M(m,![]() m+2),
m+2),
∴PM=![]() ,
,
∵PM∥y轴,PQ∥x轴
∴PM⊥PQ
当0<m≤1时,PQ=2﹣2m,
∴![]() =2﹣2m,
=2﹣2m,
解得m=6﹣2![]() 或6+2
或6+2![]() (不符合题意舍去);
(不符合题意舍去);
当1<m<4时,PQ=﹣2+2m,
∴![]() =﹣2+2m,
=﹣2+2m,
解得m=2![]() ﹣2或﹣2
﹣2或﹣2![]() ﹣2(不符合题意舍去).
﹣2(不符合题意舍去).
综上,m为6﹣2![]() 或2
或2![]() ﹣2时,△PMQ为等腰直角三角形.
﹣2时,△PMQ为等腰直角三角形.

 名校课堂系列答案
名校课堂系列答案【题目】为了解学生每天的睡眠情况,某初中学校从全校 800 名学生中随机抽取了 40 名学生,调查了他们平均每天的睡眠时间(单位: h) ,统计结果如下:
9,8,10.5,7,9,8,10,9.5,8,9,9.5,7.5,9.5,9,8.5,7.5,10,9.5,8,9,
7,9.5,8.5,9,7,9,9,7.5,8.5,8.5,9,8,7.5,9.5,10,9.5,8.5,9,8,9.
在对这些数据整理后,绘制了如下的统计图表:
睡眠时间分组统计表 睡眠时间分布情况
组别 | 睡眠时间分组 | 人数(频数) |
1 | 7≤t<8 | m |
2 | 8≤t<9 | 11 |
3 | 9≤t<10 | n |
4 | 10≤t<11 | 4 |

请根据以上信息,解答下列问题:
(1) m = , n = , a = , b = ;
(2)抽取的这 40 名学生平均每天睡眠时间的中位数落在 组(填组别) ;
(3)如果按照学校要求,学生平均每天的睡眠时间应不少于 9 h,请估计该校学生中睡眠时间符合要求的人数.
【题目】某市水费采用阶梯收费制度,即:每月用水不超过15吨时,每吨需缴纳水费a元,每月用水量超过15吨时,超过15吨的部分按每吨提高b元缴纳下表是嘉琪家一至四月份用水量和缴纳水费情况.根据表格提供的数据,回答:
月份 | 一 | 二 | 三 | 四 |
月用水量(吨) | 14 | 18 | 16 | 13 |
水费(元) | 42 | 60 | 50 | 39 |
(1)a= 元;b= 元;
(2)求月缴纳水费p(元)与月用水量t(吨)之间的函数关系式;
(3)若嘉琪家五月和六月的月缴水费相差24元,求这两月用水量差的最小值.