��Ŀ����
����Ŀ����ƽ��ֱ������ϵxOy�У����κ���y=�� ![]() x2+
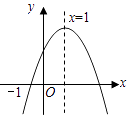
x2+ ![]() x+2��ͼ����x�ύ�ڵ�A��B����B�ڵ�A����ࣩ����y�ύ�ڵ�C��������H��0��m����ƽ����x���ֱ��l��ֱ��l����κ���y=��
x+2��ͼ����x�ύ�ڵ�A��B����B�ڵ�A����ࣩ����y�ύ�ڵ�C��������H��0��m����ƽ����x���ֱ��l��ֱ��l����κ���y=�� ![]() x2+
x2+ ![]() x+2��ͼ���ཻ�ڵ�D��E��
x+2��ͼ���ཻ�ڵ�D��E��
��1��д����A����B�����ꣻ
��2����m��0����DEΪֱ������Q������Q��x������ʱ����m��ֵ��
��3��ֱ��l���Ƿ����һ��F��ʹ�á�ACF�ǵ���ֱ�������Σ������ڣ���m��ֵ���������ڣ���˵�����ɣ�
���𰸡�
��1��
�⣺��y=0ʱ���� ![]() ��
��
��ã�x1=4��x2=��1��
��A��B���������ֱ�Ϊ��4��0���ͣ���1��0����
��2��
�⣺�ߡ�Q��x�����У����� ![]() ����D��E���㣬
����D��E���㣬
��Բ��Qλ��ֱ���������߶Գ���Ľ��㴦��
�������ߵĶԳ���Ϊ  ����Q�İ뾶ΪH���������m��m��0����
����Q�İ뾶ΪH���������m��m��0����
��D��E���������ֱ�Ϊ���� ![]() ��m��m������
��m��m������ ![]() +m��m��
+m��m��
��E���ڶ��κ��� ![]() ��ͼ���ϣ�
��ͼ���ϣ�
�� ![]() ��
��
��� ![]() ��
�� ![]() ���������⣬��ȥ����
���������⣬��ȥ����
��3��
�⣺���ڣ�
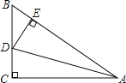
����ͼ1��

����ACF=90�㣬AC=FCʱ������F��FG��y����G��
���AOC=��CGF=90�㣬
�ߡ�ACO+��FCG=90�㣬��GFC+��FCG=90�㣬
���ACO=��CFG��
���ACO�ա�CFG��
��CG=AO=4��
��CO=2��
��m=OG=2+4=6��
�����ӳ�FC��ʹ��CF=CF�䣬��ʱ��ACF����Ϊ����ֱ�������Σ�
��yC��yF��=CG=4��
��m=CO��4=2��4=��2��
����ͼ2��

����CAF=90�㣬AC=AFʱ������F��FP��x����P��
�ߡ�AOC=��APF=90�㣬��ACO+��OAC=90�㣬��FAP+��OAC=90�㣬
���ACO=��FAP��
���ACO�ա���FAP��
��FP=AO=4��
��m=FP=4��
�����ӳ�FA��ʹ��AF=AF�䣬��ʱ��ACF����Ϊ����ֱ�������Σ�
��yA��yF��=FP=4��
��m=0��4=��4��
����ͼ3��

����AFC=90�㣬FA=FCʱ����F��һ����AC���д����ϣ���ʱ����������ֱ��ΪF��F�䣬
�ֱ��F��F��������x�ᡢy��Ĵ��ߣ��ֱ���E��G��D��H��
�ߡ�DFC+��CFE=��CFE+��EFA=90�㣬
���DFC=��EFA��
�ߡ�CDF=��AEF��CF=AF��
���CDF�ա�AEF��
��CD=AE��DF=EF��
���ı���OEFDΪ�����Σ�
��OA=OE+AE=OD+AE=OC+CD+AE=OC+2CD��
��4=2+2CD��
��CD=1��
��m=OC+CD=2+1=3��
�ߡ�HF��C+��CGF��=��CF��G+��GF��A��
���HF��C=��GF��A��
�ߡ�HF��C=��GF��A��CF��=AF�䣬
���HF��C�ա�GF��A��
��HF��=GF�䣬CH=AG��
���ı���OHF��GΪ�����Σ�
��OH=CH��CO=AG��CO=AO��OG��CO=AO��OH��CO=4��OH��2��
��OH=1��
��m=��1��
��y=�� ![]() x2+
x2+ ![]() x+2=��
x+2=�� ![]() ��x��
��x�� ![]() ��2+
��2+ ![]() ��
��
��y�����ֵΪ ![]() ��
��
��ֱ��l�����������������㣬��m�� ![]() ��
��
��m��ȡֵΪ����4����2����1��3��
����������ֱ��l�ϴ�һ��F��ʹ�á�ACF�ǵ���ֱ�������Σ�m��ֵΪ��4����2����1��3��
����������1��A��B����������궼Ϊ0�����Դ���y=0����⼴�ɣ���2����Բ��������������Բ��Qλ��ֱ���������߶Գ���Ľ��㴦����Q�ĺ�����Ϊ ![]() �����Ƴ�D��E���������ֱ�Ϊ����
�����Ƴ�D��E���������ֱ�Ϊ���� ![]() ��m��m������
��m��m������ ![]() +m��m������ΪD��E�����������ϣ�����һ�㼴�ɵ�m����3��ʹ�á�ACF�ǵ���ֱ�������Σ��ص����Ҫ�����м������Σ��ֱ�������Ϊ���������ε��������ߵף�����3�����Σ�������������F����AC�����»����Ϸ��ָ�����2�����Σ��ʹ���6�����Σ����ʱ������ȫ��������֪ʶ��m��ֵ��
+m��m������ΪD��E�����������ϣ�����һ�㼴�ɵ�m����3��ʹ�á�ACF�ǵ���ֱ�������Σ��ص����Ҫ�����м������Σ��ֱ�������Ϊ���������ε��������ߵף�����3�����Σ�������������F����AC�����»����Ϸ��ָ�����2�����Σ��ʹ���6�����Σ����ʱ������ȫ��������֪ʶ��m��ֵ��
�����㾫����������Ŀ����֪���������ö��κ�����ͼ��Ͷ��κ��������ʵ����֪ʶ���Եõ�����Ĵ𰸣���Ҫ���ն��κ���ͼ��ؼ��㣺1�����ڷ���2���Գ��� 3������ 4����x�ύ�� 5����y�ύ�㣻�����ԣ���a>0ʱ���Գ�����ߣ�y��x�������С���Գ����ұߣ�y��x���������a<0ʱ���Գ�����ߣ�y��x��������Գ����ұߣ�y��x�������С��

 ��ʱѵ���������������ϵ�д�
��ʱѵ���������������ϵ�д� �ƸԾ���Ȥζ����ϵ�д�
�ƸԾ���Ȥζ����ϵ�д� ����С����ҵ��ϵ�д�
����С����ҵ��ϵ�д�