题目内容
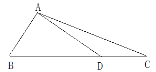
【题目】如图,AB是半圆O的直径,D为BC的中点,连接OD并延长,交弧BC于点E,F为OD延长线上一点且满足∠OFC=∠ABC.
(1)试判断CF与⊙O的位置关系,并说明理由;
(2)若∠ABC=30°,求sin∠DAO的值.

【答案】(1)CF是⊙O的切线,理由详见解析;(2)![]() .
.
【解析】
(1)欲证明CF为⊙O的切线,只要证明即OC⊥CF即可.
(2)设⊙O的半径为r.由OD⊥BC 且∠ABC=30°,可得OD=![]() OB=
OB=![]() r,作DH⊥AB于H,求出DH、AD即可解决问题.
r,作DH⊥AB于H,求出DH、AD即可解决问题.
(1)结论:CF是⊙O的切线.
理由:连接CO.
∵D为BC的中点,且OB=OC,
∴OD⊥BC,
∵OB=OC,
∴∠OBC=∠OCB,
又∵∠OBC=∠OFC,
∴∠OCB=∠OFC,
∵OD⊥BC,
∴∠DCF+∠OFC=90°.
∴∠DCF+∠OCB=90°.即OC⊥CF,
∴CF为⊙O的切线.
(2)①设⊙O的半径为r.如图,作DH⊥AB于H,

∵OD⊥BC 且∠ABC=30°,
∴OD=![]() OB=
OB=![]() r,
r,
在Rt△ODH中,∠DOH=60°,OD=![]() r.
r.
∴DH=![]() r,OH=
r,OH=![]() r,
r,
在Rt△DAH中,∵AH=AO+OH=![]() r,
r,
∴由勾股定理:![]() .
.
∴ .
.

练习册系列答案
相关题目