题目内容
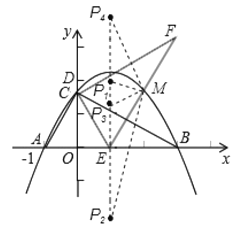
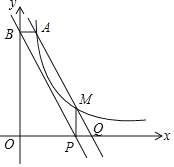
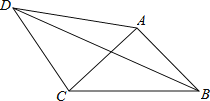
【题目】在平面直角坐标系xOy中,一块含60°角的三角板作如图摆放,斜边AB在x轴上,直角顶点C在y轴正半轴上,已知点A(﹣1,0).
(1)请直接写出点B、C的坐标:B( )、C( );并求经过A、B、C三点的抛物线解析式;
(2)现有与上述三角板完全一样的三角板DEF(其中∠EDF=90°,∠DEF=60°),把顶点E放在线段AB上(点E是不与A、B两点重合的动点),并使ED所在直线经过点C.此时,EF所在直线与(1)中的抛物线交于点M.
①设AE=x,当x为何值时,△OCE∽△OBC;
②在①的条件下探究:抛物线的对称轴上是否存在点P使△PEM是等腰三角形?若存在,请写出点P的坐标;若不存在,请说明理由.

【答案】(1)![]() ,
,![]() ,抛物线解析式为
,抛物线解析式为![]() ;
;
(2)①当![]() 时,△OCE∽△OBC;②抛物线对称轴上存在点P
时,△OCE∽△OBC;②抛物线对称轴上存在点P![]() 或
或![]() 或
或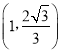 或
或![]() ,使△PEM是等腰三角形.
,使△PEM是等腰三角形.
【解析】
(1)利用解直角三角形求出OC的长度,再求出OB的长度,从而可得点B、C的坐标,然后利用待定系数法求二次函数解析式解答;
(2)①根据相似三角形对应边成比例列式求出OE的长度,再根据点A的坐标求出AO的长度,相加即可得到AE的长度,即x的值;
②根据①确定点E在对称轴上,然后求出∠FEB=60°,根据同位角相等两直线平行求出EF//AC,再求出直线EF的解析式,与抛物线解析式联立求出点M的坐标,再利用两点间的距离公式求出EM的长度,再分PE=EM,PE=PM,PM=EM三种情况分别求解.
(1)∵点![]()
∴![]()
由图可知,∠BAC是三角板的60°角,∠ABC是30°角
∴![]() ,
,![]()
∴点![]() ,点
,点![]()
设抛物线解析式为![]()
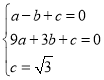
解得![]()
∴抛物线解析式为![]()
(2)①∵△OCE∽△OBC
∴![]()
即![]()
解得![]()
∴![]()
即![]() 时,△OCE∽△OBC
时,△OCE∽△OBC
②存在,理由如下:
抛物线的对称轴为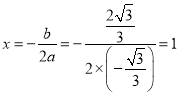
∴点E为抛物线的对称轴与x轴的交点
∵![]() ,
,![]() 轴,
轴,![]()
∴△ACE是等边三角形
∴![]()
∵![]()
∴![]()
∴![]()
∴![]()
由![]() 可得直线AC的解析式为
可得直线AC的解析式为![]()
∵点E![]()
∴直线EF的解析式为![]()
联立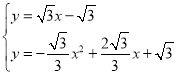
解得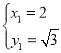 ,
,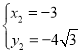
∴点M的坐标为![]() 或
或![]() (舍去)
(舍去)
![]()
分三种情况讨论△PEM是等腰三角形
1)当![]() 时,
时,![]()
∴点P的坐标为![]() 或
或![]()
2)当![]() 时,
时,
∵![]()
∴![]()
![]()
![]()
![]()
∴点P的坐标为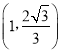
3)当![]() 时,
时,![]()
∴点P的坐标为![]()
综上所述,抛物线对称轴上存在点P![]() 或
或![]() 或
或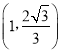 或
或![]() ,使△PEM是等腰三角形.
,使△PEM是等腰三角形.