题目内容
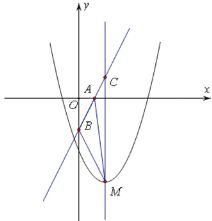
【题目】已知二次函数![]() 的图象( 记为抛物线
的图象( 记为抛物线![]() ) 顶点为M,直线
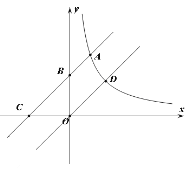
) 顶点为M,直线![]() :y=2x-a与x轴,y轴分别交于点A,B.
:y=2x-a与x轴,y轴分别交于点A,B.
(1)若抛物线![]() 与x轴只有一个公共点,求a的值;
与x轴只有一个公共点,求a的值;
(2)当a>0时,设△ABM的面积为S,求S与a的函数关系式;
(3)将二次函数![]() 的图象
的图象![]() 绕点P(t,-2)旋转180°得到二次函数的图象记为抛物线
绕点P(t,-2)旋转180°得到二次函数的图象记为抛物线![]() ,顶点为N。
,顶点为N。
①若点N恰好落在直线![]() 上,求a 与t 满足的关系;
上,求a 与t 满足的关系;
②当-2≤x≤1时,旋转前后的两个二次函数y的值都会随x的值得增大而减小,求t 的取值范围.
【答案】(1)a=-2;(2)S=a;(3)①a=2t;②t≤![]() .
.
【解析】
(1)抛物线与x轴只有一个交点,即只有顶点M在x轴上,故M的纵坐标为0;
(2)设直线![]() 与二次函数
与二次函数![]() 的图象
的图象![]() 的对称轴x=1交于点C,则C(1,2-a),根据S=
的对称轴x=1交于点C,则C(1,2-a),根据S=![]() 即可得S与a的函数关系式;
即可得S与a的函数关系式;
(3)①根据题意,点M绕点P(t,-2)旋转180°得到点N,所以MP=NP,即P为MN中点,根据中点坐标公式可得点N的坐标(2t-1,a-2),代入直线![]() :y=2x-a即可求a与t的关系式;
:y=2x-a即可求a与t的关系式;
②旋转前的抛物线对称轴为直线x=1,要满足在-2≤x≤1时y随x的增大而减小,即在对称轴左侧抛物线下降,故开口向上;则旋转后的抛物线开口向下,对称轴必须在x=-2的左侧,即求出t的范围.
解:(1)![]()
抛物线![]() 的顶点M的坐标为(1,-a-2).
的顶点M的坐标为(1,-a-2).
∵二次函数的图象![]() 与x轴只有一个公共点
与x轴只有一个公共点
∴顶点M在x轴上
∴-a-2=0,
∴a=-2 ;
(2)∵y=2x-a与x、y轴分别交于A、B两点
∴A(![]() ,0),B(0,
,0),B(0,![]() )
)
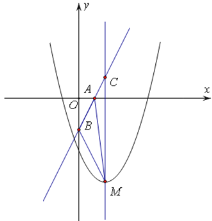
设直线![]() 与二次函数
与二次函数![]() 的图象
的图象![]() 的对称轴x=1交于点C,则C(1,2-a),CM=(2-a)-(-a-2)=4
的对称轴x=1交于点C,则C(1,2-a),CM=(2-a)-(-a-2)=4
∴S=![]() ;
;
(3)①根据题意得,抛物线![]() 的顶点N与抛物线
的顶点N与抛物线![]() 的顶点M关于P(t,-2)成中心对称,
的顶点M关于P(t,-2)成中心对称,
∴顶点N坐标为(2t-1a-2)
∵点N恰好落在直线![]() 上
上
∴a-2=2(2t-1)-a
∴a=2t ;
②∵旋转前抛物线对称轴为直线x=1
∴当a>0抛物线开口向上时,当-2≤x≤1时,抛物线![]() 的y的值随x的值增大而减小
的y的值随x的值增大而减小
∴旋转后抛物线开口向下,且顶点N(2t-1,a-2)
∵要满足在-2≤x<1的范围内y随x增大而减小,即抛物线下降
∴对称轴直线x=2t-1需在x=-2左侧
∴2t-1≤-2
解得:t≤![]()
∴当t≤![]() 时抛物线
时抛物线![]() 的y的值随x的值增大而减小.
的y的值随x的值增大而减小.
故答案为:(1)a=-2;(2)S=a;(3)①a=2t;②t≤![]() .
.