题目内容
【题目】在数学课上,同学们已经探究过“经过已知直线外一点作这条直线的垂线”的尺规作图:
已知:直线l和l外一点P.

求作:直线l的垂线,使它经过点P.
做法:如图:(1)在直线l上任取两点A、B;
(2)分别以点A、B为圆心,![]() 、
、![]() 长为半径画弧,两弧相交于点Q;
长为半径画弧,两弧相交于点Q;
(3)作直线![]() .
.
参考以上材料作图的方法,解决以下问题:
(1)以上材料作图的依据是__________________.
(2)已知:直线l和l外一点P.
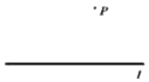
求作:![]() ,使它与直线l相切于点C(尺规作图,不写作法,保留作图痕迹).
,使它与直线l相切于点C(尺规作图,不写作法,保留作图痕迹).
(3)完成下面的证明.
证明:∵![]() _____________,且
_____________,且![]() ___________.
___________.
∴直线l是P的切线(_____________________)(填推理的依据).
【答案】(1)垂直平分线上的点到线段两端距离相等;
(2)见解析;
(3)![]() ;
;![]() 为半径;过半径外端且垂直于这条半径的直线是圆的切线.
为半径;过半径外端且垂直于这条半径的直线是圆的切线.
【解析】
(1)由AP=AQ,BP=PQ可知,AB为PQ的垂直平分线,根据线段的垂直平分线的判定定理的逆定理可判断PQ![]() ;
;
(2)按照材料的作图方法,先过点P作直线![]() 的垂线,交AB于C;再根据“过半径外端且垂直于这条半径的直线是圆的切线”可知,以PC为半径作圆,
的垂线,交AB于C;再根据“过半径外端且垂直于这条半径的直线是圆的切线”可知,以PC为半径作圆,![]() 与直线l相切于点C.
与直线l相切于点C.
(3)利用![]() ,PC为半径,再根据切线的判定定理可判断直线l是
,PC为半径,再根据切线的判定定理可判断直线l是![]() 的切线.
的切线.
(1) 垂直平分线上的点到线段两端距离相等;
(2)如图所示:
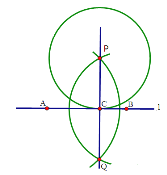
(3)∵![]() ,且
,且![]() 为半径.
为半径.
∴直线l是P的切线(过半径外端且垂直于这条半径的直线是圆的切线)

【题目】已知抛物线y=-x2-2x+c与x轴的一个交点是(1,0).
(1)C的值为_______;
(2)选取适当的数据补填下表,并在平面直角坐标系内描点画出该抛物线的图像;
|
|
|
|
| |||
|
|
|
|
(3)根据所画图像,写出y>0时x的取值范围是_____.