题目内容
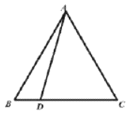
【题目】如图,等边三角形![]() 中,D是
中,D是![]() 上一点,连接
上一点,连接![]() 并将
并将![]() 绕点A逆时针旋转120°得到线段
绕点A逆时针旋转120°得到线段![]() ,连接
,连接![]() 交
交![]() 于点F.
于点F.
(1)当点D为![]() 中点,且
中点,且![]() 时,
时,![]() ___________;
___________;
(2)补全图形,探究线段![]() 与
与![]() 之间的数量关系,并证明你的结论.
之间的数量关系,并证明你的结论.
【答案】(1)![]() ;(2)
;(2)![]() ,证明见详解.
,证明见详解.
【解析】
(1)作![]() ,交CA的延长线于G,根据等边三角形的性质得出∠CAD=30°, AD⊥BC,进而求得BD=CD=1,等边三角形边长为2,易证得△AGE≌△DBA,GE=BC,AG=BD=1, 然后根据平行线分,线段成比例定理求得GF=FC=
,交CA的延长线于G,根据等边三角形的性质得出∠CAD=30°, AD⊥BC,进而求得BD=CD=1,等边三角形边长为2,易证得△AGE≌△DBA,GE=BC,AG=BD=1, 然后根据平行线分,线段成比例定理求得GF=FC=![]() ,即可求得AF;
,即可求得AF;
(2)作![]() ,交CA的延长线于G,根据等边三角形的性质得出三角相等,进而求得∠ADB=∠EAG,易证得△AGE≌△DBA,证得GE=BC, AG=BD,然后根据平行线分线段成比例定理求得GF=FC,即可求得AF=
,交CA的延长线于G,根据等边三角形的性质得出三角相等,进而求得∠ADB=∠EAG,易证得△AGE≌△DBA,证得GE=BC, AG=BD,然后根据平行线分线段成比例定理求得GF=FC,即可求得AF=![]() CD.
CD.
(1)如图所示,作![]() ,交CA的延长线于G,
,交CA的延长线于G,
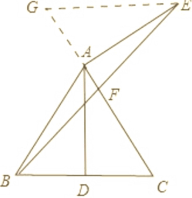
![]() 等边三角形
等边三角形![]() 中,点D为
中,点D为![]() 中点,
中点,
![]()
![]()
![]()
在![]() 和
和![]() 中,
中,
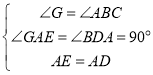
![]() ,
,
![]()
![]() ,
,
![]() ,
,
![]()
(2) ![]()

如图所示,作![]() 交CA延长线于G,
交CA延长线于G,
![]() ,
,
![]()
![]() ,
,
![]() ,
,![]()
在![]() 和
和![]() 中,
中,
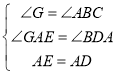
![]()
![]()
![]()
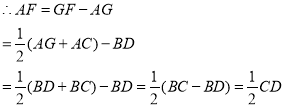
即![]() .
.

练习册系列答案
相关题目