题目内容
如图,当x=2时,抛物线 取得最小值-1,并且与y轴交于点C(0,3),与x轴交于点A、B(A在B的右边)。
取得最小值-1,并且与y轴交于点C(0,3),与x轴交于点A、B(A在B的右边)。
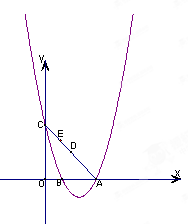
(1)求抛物线的解析式;
(2)D是线段AC的中点,E为线段AC上的一动点(不与A,C重合),过点E作y轴的平行线EF与抛物线交于点F。问:是否存在△DEF与△AOC相似?若存在,求出点E的坐标;若不存在,请说明理由;
(3)在抛物线的对称轴上是否存在点P,使得△APD为等腰三角形?若存在,请直接写出点p的坐标;若不存在,请说明理由。
 取得最小值-1,并且与y轴交于点C(0,3),与x轴交于点A、B(A在B的右边)。
取得最小值-1,并且与y轴交于点C(0,3),与x轴交于点A、B(A在B的右边)。
(1)求抛物线的解析式;
(2)D是线段AC的中点,E为线段AC上的一动点(不与A,C重合),过点E作y轴的平行线EF与抛物线交于点F。问:是否存在△DEF与△AOC相似?若存在,求出点E的坐标;若不存在,请说明理由;
(3)在抛物线的对称轴上是否存在点P,使得△APD为等腰三角形?若存在,请直接写出点p的坐标;若不存在,请说明理由。
(1)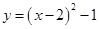 ;(2)
;(2)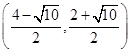 或
或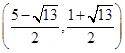 ;(3)
;(3)
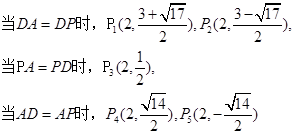
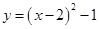 ;(2)
;(2)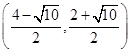 或
或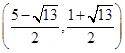 ;(3)
;(3)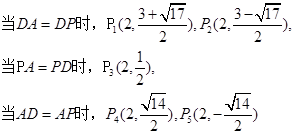
试题分析:(1)已知,当x=2时,抛物线的最小值为-1,因此抛物线的顶点坐标为(2,-1);可用顶点式来设抛物线的解析式,然后将C的坐标代入即可求出抛物线的解析式.
(2)由于EF∥OC,那么∠FED=45°,因此要使三角形EFD与三角形COA相似,只有两种情况:当D为直角顶点时,∠EDF=90°,由于D是AC中点,而FD⊥AC,三角形AOC又是个等腰直角三角形,因此DF正好在∠COA的平分线上,即DF在直线y=x上,此时可先求出直线AC的函数关系式,然后联立抛物线的解析式求出F的坐标,由于E、F的横坐标相同,将F的横坐标代入AC所在的直线的解析式中即可求出E点的坐标.
(3)当F为直角顶点时,∠EFD=90°,那么DF与三角形AOC的中位线在同一直线上,即DF所在的直线的解析式为y=2,然后可根据(2)的方法求出p点的坐标.
(1)由题意可设抛物线的关系式为
y=a(x-2)2-1
因为点C(0,3)在抛物线上
所以3=a(0-2)2-1,即a=1
所以,抛物线的关系式为
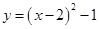 ;
;(2)令y=0,即x2-4x+3=0,
得点A(3,0),B(1,0),线段AC的中点为D(
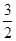 ,
,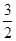 )
)直线AC的函数关系式为y=-x+3
因为△OAC是等腰直角三角形,
所以,要使△DEF与△AOC相似,△DEF也必须是等腰直角三角形.
由于EF∥OC,因此∠DEF=45°,
所以,在△DEF中只可能以点D、F为直角顶点.
当F为直角顶点时,DF⊥EF,此时△DEF∽△ACO,DF所在直线为y=
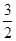
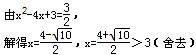
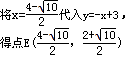
当D为直角顶点时,DF⊥AC,此时△DEF∽△OAC,由于点D为线段AC的中点,
因此,DF所在直线过原点O,其关系式为y=x.
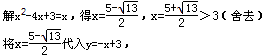
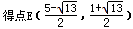
当∠DFE=90°时,E1
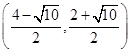 ,当∠EDF=90°时,E2
,当∠EDF=90°时,E2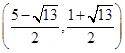 ;
;(3)
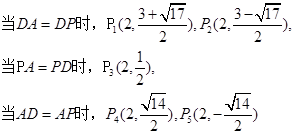
点评:解题的关键是要注意的是(3)中在不确定△EDF的直角顶点的情况下要分类进行讨论,不要漏解.

练习册系列答案
 全能练考卷系列答案
全能练考卷系列答案
相关题目
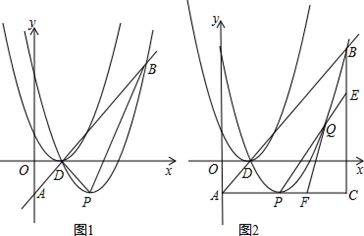
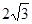 ),∠BCO=60°,OH⊥BC于点H.动点P从点H出发,沿线段HO向点O运动,动点Q从点O出发,沿线段OA向点A运动,两点同时出发,速度都为每秒1个单位长度.设点P运动的时间为t秒.
),∠BCO=60°,OH⊥BC于点H.动点P从点H出发,沿线段HO向点O运动,动点Q从点O出发,沿线段OA向点A运动,两点同时出发,速度都为每秒1个单位长度.设点P运动的时间为t秒.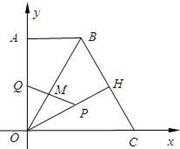
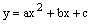 与x轴的另一交点为A,顶点为P,且对称轴为直线x=2.
与x轴的另一交点为A,顶点为P,且对称轴为直线x=2.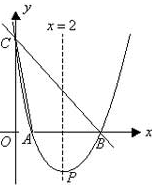
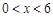 )的小正方形,如果设剩余部分的面积为y,那么y关于x的函数解析式为 .
)的小正方形,如果设剩余部分的面积为y,那么y关于x的函数解析式为 .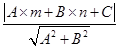 .
.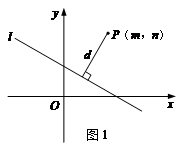
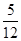 x-
x-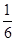 的距离d时,先将y=
的距离d时,先将y=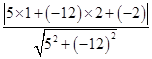 =
=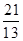 .
.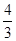 x-4与x轴交于点A,与y轴交于点B,抛物线y=x2-4x+5上的一点M(3,2).
x-4与x轴交于点A,与y轴交于点B,抛物线y=x2-4x+5上的一点M(3,2).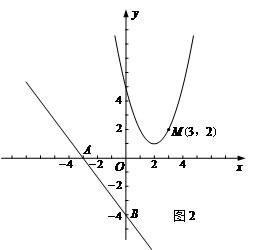
 经过梯形的顶点A、B、C、D,已知梯形的两条底边长分别为4,6,该抛物线解析式为________________
经过梯形的顶点A、B、C、D,已知梯形的两条底边长分别为4,6,该抛物线解析式为________________