题目内容
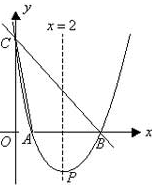
如图,直线y= -x+3与x轴,y轴分别相交于点B、C,经过B、C两点的抛物线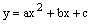 与x轴的另一交点为A,顶点为P,且对称轴为直线x=2.
与x轴的另一交点为A,顶点为P,且对称轴为直线x=2.
(1)求A点的坐标;
(2)求该抛物线的函数表达式;
(3)连结AC.请问在x轴上是否存在点Q,使得以点P、B、Q为顶点的三角形与△ABC 相似,若存在,请求出点Q的坐标;若不存在,请说明理由.
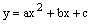 与x轴的另一交点为A,顶点为P,且对称轴为直线x=2.
与x轴的另一交点为A,顶点为P,且对称轴为直线x=2.
(1)求A点的坐标;
(2)求该抛物线的函数表达式;
(3)连结AC.请问在x轴上是否存在点Q,使得以点P、B、Q为顶点的三角形与△ABC 相似,若存在,请求出点Q的坐标;若不存在,请说明理由.
(1)(1,0)(2)y=2x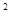 -4x-6 (3)存在
-4x-6 (3)存在
 -4x-6 (3)存在
-4x-6 (3)存在试题分析:【探究】证明:过点F作GH∥AD,交AB于H,交DC的延长线于点G
∵AH∥EF∥DG,AD∥GH
∴四边形AHFE和四边形DEFG都是平行四边形
∴FH=AE,FG=DE
∵AE=DE
∴FG=FH
∵AB∥DG
∴∠G=∠FHB,∠GCF=∠B
∴△CFG≌△BFH
∴FC=FB 4分
【知识应用】过点C作CM⊥x轴于点M,过点A作AN⊥x轴于点N,过点B作BP⊥x轴于点P
则点P的坐标为(x
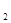 ,0),点N的坐标为(x
,0),点N的坐标为(x ,0)
,0)由探究的结论可知,MN=MP
∴点M的坐标为(
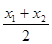 ,0)
,0)∴点C的横坐标为
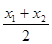
同理可求点C的纵坐标为

∴点C的坐标为(
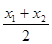 ,
,
 ) 8分
) 8分【知识拓展】
当AB是平行四边形一条边,且点C在x轴的正半轴时,AD与BC互相平分,设点C的坐标为(a,0),点D的坐标为(0,y)
由上面的结论可知:-6+a=4+0,-1+0=5+b
∴a=10,b=-6
∴此时点C的坐标为(10,0),点D的坐标为(0,-6)
同理,当AB是平行四边形一条边,且点C在x轴的负半轴时
求得点C的坐标为(-10,0),点D的坐标为(0,6)
当AB是对角线时
点C的坐标为(-2,0),点D的坐标为(0,4) 14
点评:本题考查抛物线的知识,要求考生会用待定系数法求抛物线的解析式,掌握抛物线的性质

练习册系列答案
 百年学典课时学练测系列答案
百年学典课时学练测系列答案
相关题目
 ,在平面直角坐标系中,等腰直角
,在平面直角坐标系中,等腰直角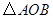 的斜边
的斜边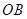 在
在 轴上,顶点
轴上,顶点 的坐标为
的坐标为 ,
,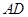 为斜边上的高.抛物线
为斜边上的高.抛物线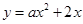 与直线
与直线 交于点
交于点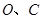 ,点
,点 的横坐标为
的横坐标为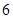 .点
.点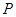 在
在 轴.交射线
轴.交射线 于点
于点 .设点
.设点 ,以
,以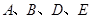 为顶点的四边形的面积为
为顶点的四边形的面积为 .
.
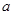 的值;
的值;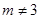 时,求
时,求 ,设直线
,设直线 交射线
交射线 于点
于点 ,交抛物线于点
,交抛物线于点 .以
.以 为一边,在
为一边,在 ,其中
,其中 .直接写出矩形
.直接写出矩形 取得最小值-1,并且与y轴交于点C(0,3),与x轴交于点A、B(A在B的右边)。
取得最小值-1,并且与y轴交于点C(0,3),与x轴交于点A、B(A在B的右边)。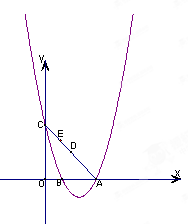

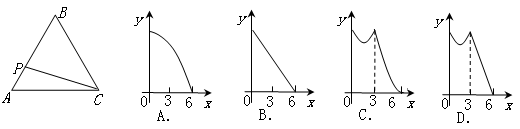
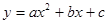 的部分图象如图所示,由图象可知该二次函数的图象的对称轴是直线x= .
的部分图象如图所示,由图象可知该二次函数的图象的对称轴是直线x= .
 -2实数根的情况是
-2实数根的情况是