题目内容
在四边形ABDE中,C是BD边的中点.
(1)如图(1),若AC平分∠BAE,∠ACE=90°,则线段AE、AB、DE的长度满足的数量关系为
;(直接写出答案)
(2)如图(2),AC平分∠BAE,EC平分∠AED,若∠ACE=120°,则线段AB、BD、DE、AE的长度满足怎样的数量关系?写出结论并证明;
(3)如图(3),如图(3),BD=8,AB=2,DE=8,若ACE=135°,则线段AE长度的最大值是 (直接写出答案).

(1)如图(1),若AC平分∠BAE,∠ACE=90°,则线段AE、AB、DE的长度满足的数量关系为
(2)如图(2),AC平分∠BAE,EC平分∠AED,若∠ACE=120°,则线段AB、BD、DE、AE的长度满足怎样的数量关系?写出结论并证明;
(3)如图(3),如图(3),BD=8,AB=2,DE=8,若ACE=135°,则线段AE长度的最大值是

考点:全等三角形的判定与性质,等边三角形的判定与性质
专题:
分析:(1)在AE上取一点F,使AF=AB,及可以得出△ACB≌△ACF,就可以得出BC=FC,∠ACB=∠ACF,就可以得出△CEF≌△CED.就可以得出结论;
(2)在AE上取点F,使AF=AB,连结CF,在AE上取点G,使EG=ED,连结CG.可以求得CF=CG,△CFG是等边三角形,就有FG=CG=
BD,进而得出结论;
(3)在AE上取点F,使AF=AB,连结CF,在AE上取点G,使EG=ED,连结CG.可以求得CF=CG,△CFG是等腰直角三角形,由勾股定理求出FG的值就可以得出结论.
(2)在AE上取点F,使AF=AB,连结CF,在AE上取点G,使EG=ED,连结CG.可以求得CF=CG,△CFG是等边三角形,就有FG=CG=
| 1 |
| 2 |
(3)在AE上取点F,使AF=AB,连结CF,在AE上取点G,使EG=ED,连结CG.可以求得CF=CG,△CFG是等腰直角三角形,由勾股定理求出FG的值就可以得出结论.
解答:解:(1)AE=AB+DE;
理由:在AE上取一点F,使AF=AB.
∵AC平分∠BAE,
∴∠BAC=∠FAC.
在△ACB和△ACF中,
,
∴△ACB≌△ACF(SAS),
∴BC=FC,∠ACB=∠ACF.
∵C是BD边的中点.
∴BC=CD,
∴CF=CD.
∵∠ACE=90°,
∴∠ACB+∠DCE=90°,∠ACF+∠ECF=90°
∴∠ECF=∠ECD.
在△CEF和△CED中,
,
∴△CEF≌△CED(SAS),
∴EF=ED.
∵AE=AF+EF,
∴AE=AB+DE;
故答案为:AE=AB+DE

(2)猜想:AE=AB+DE+
BD.
证明:在AE上取点F,使AF=AB,连结CF,在AE上取点G,使EG=ED,连结CG.

∵C是BD边的中点,
∴CB=CD=
BD.
∵AC平分∠BAE,
∴∠BAC=∠FAC.
在△ACB和△ACF中,
,
∴△ACB≌△ACF(SAS),
∴CF=CB,∴∠BCA=∠FCA.
同理可证:CD=CG,∴∠DCE=∠GCE.
∵CB=CD,∴CG=CF
∵∠ACE=120°,
∴∠BCA+∠DCE=180°-120°=60°.
∴∠FCA+∠GCE=60°.
∴∠FCG=60°.
∴△FGC是等边三角形.
∴FG=FC=
BD.
∵AE=AF+EG+FG.
∴AE=AB+DE+
BD.
(3)在AE上取点F,使AF=AB,连结CF,在AE上取点G,使EG=ED,连结CG.
∵C是BD边的中点,
∴CB=CD=
BD.
∵AC平分∠BAE,
∴∠BAC=∠FAC.
在△ACB和△ACF中,
,
∴△ACB≌△ACF(SAS),
∴CF=CB,∴∠BCA=∠FCA.
同理可证:CD=CG,∴∠DCE=∠GCE.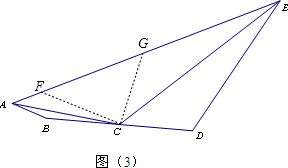
∵CB=CD,∴CG=CF
∵∠ACE=135°,
∴∠BCA+∠DCE=180°-135°=45°.
∴∠FCA+∠GCE=45°.
∴∠FCG=90°.
∴△FGC是等腰直角三角形.
∴FC=
BD.
∵BD=8,
∴FC=4,
∴FG=4
.
∵AE=AF+FG+GE,
∴AE=AB+4
+DE.
∵AB=2,DE=8,
∴AE≤AF+FG+EG=10+4
.
故答案为:10+4
.
理由:在AE上取一点F,使AF=AB.
∵AC平分∠BAE,
∴∠BAC=∠FAC.
在△ACB和△ACF中,
|
∴△ACB≌△ACF(SAS),
∴BC=FC,∠ACB=∠ACF.
∵C是BD边的中点.
∴BC=CD,
∴CF=CD.
∵∠ACE=90°,
∴∠ACB+∠DCE=90°,∠ACF+∠ECF=90°
∴∠ECF=∠ECD.
在△CEF和△CED中,
|
∴△CEF≌△CED(SAS),
∴EF=ED.
∵AE=AF+EF,
∴AE=AB+DE;
故答案为:AE=AB+DE

(2)猜想:AE=AB+DE+
| 1 |
| 2 |
证明:在AE上取点F,使AF=AB,连结CF,在AE上取点G,使EG=ED,连结CG.

∵C是BD边的中点,
∴CB=CD=
| 1 |
| 2 |
∵AC平分∠BAE,
∴∠BAC=∠FAC.
在△ACB和△ACF中,
|
∴△ACB≌△ACF(SAS),
∴CF=CB,∴∠BCA=∠FCA.
同理可证:CD=CG,∴∠DCE=∠GCE.
∵CB=CD,∴CG=CF
∵∠ACE=120°,
∴∠BCA+∠DCE=180°-120°=60°.
∴∠FCA+∠GCE=60°.
∴∠FCG=60°.
∴△FGC是等边三角形.
∴FG=FC=
| 1 |
| 2 |
∵AE=AF+EG+FG.
∴AE=AB+DE+
| 1 |
| 2 |
(3)在AE上取点F,使AF=AB,连结CF,在AE上取点G,使EG=ED,连结CG.
∵C是BD边的中点,
∴CB=CD=
| 1 |
| 2 |
∵AC平分∠BAE,
∴∠BAC=∠FAC.
在△ACB和△ACF中,
|
∴△ACB≌△ACF(SAS),
∴CF=CB,∴∠BCA=∠FCA.
同理可证:CD=CG,∴∠DCE=∠GCE.

∵CB=CD,∴CG=CF
∵∠ACE=135°,
∴∠BCA+∠DCE=180°-135°=45°.
∴∠FCA+∠GCE=45°.
∴∠FCG=90°.
∴△FGC是等腰直角三角形.
∴FC=
| 1 |
| 2 |
∵BD=8,
∴FC=4,
∴FG=4
| 2 |
∵AE=AF+FG+GE,
∴AE=AB+4
| 2 |
∵AB=2,DE=8,
∴AE≤AF+FG+EG=10+4
| 2 |
故答案为:10+4
| 2 |
点评:本题考查了角平分线的性质的运用,全等三角形的判定及性质的运用,等边三角形的性质的运用,勾股定理的运用,解答时证明三角形全等是关键.

练习册系列答案
 特高级教师点拨系列答案
特高级教师点拨系列答案
相关题目
在下列四个图形中,对称轴的条数最少的图形是( )
A、 |
B、 |
C、 |
D、 |
 下图哪一个是正方体的展开图( )
下图哪一个是正方体的展开图( )A、 |
B、 |
C、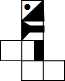 |
D、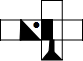 |
 如图,D是△ABC的边BC上的一点,那么下列四个条件中,不能够判定△ABC与△DBA相似的是( )
如图,D是△ABC的边BC上的一点,那么下列四个条件中,不能够判定△ABC与△DBA相似的是( )| A、∠C=∠BAD | ||||
| B、∠BAC=∠ADB | ||||
C、
| ||||
| D、AB2=BD•BC |
 如图,东西方向的海岸线上有A、B两个观测站,在A地发现它的北偏东60°方向有一条渔船C,同一时刻,在B地发现该渔船C在它的北偏西30°方向,试画图说明这条渔船的位置,并量出渔船C关于A、B两地视角(即∠ACB)的大小.
如图,东西方向的海岸线上有A、B两个观测站,在A地发现它的北偏东60°方向有一条渔船C,同一时刻,在B地发现该渔船C在它的北偏西30°方向,试画图说明这条渔船的位置,并量出渔船C关于A、B两地视角(即∠ACB)的大小.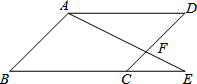 如图,?ABCD中,E为BC延长线上一点,AE交CD于点F,若
如图,?ABCD中,E为BC延长线上一点,AE交CD于点F,若