题目内容
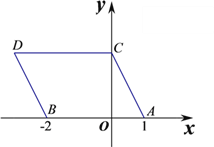
【题目】如图,在平面直角坐标系中,点![]() 的坐标分别为(1,0)、(-2,0),现同时将点
的坐标分别为(1,0)、(-2,0),现同时将点![]() 分别向上平移2个单位,再向左平移1个单位,分别得到点
分别向上平移2个单位,再向左平移1个单位,分别得到点![]() 的对应点
的对应点![]() ,连接
,连接![]() 、
、![]() 、
、![]() .
.
(1)若在![]() 轴上存在点
轴上存在点![]() ,连接
,连接![]() ,使S△ABM =S□ABDC,求出点
,使S△ABM =S□ABDC,求出点![]() 的坐标;
的坐标;
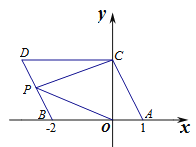
(2)若点![]() 在线段
在线段![]() 上运动,连接
上运动,连接![]() ,求S=S△PCD+S△POB的取值范围;
,求S=S△PCD+S△POB的取值范围;
(3)若![]() 在直线
在直线![]() 上运动,请直接写出
上运动,请直接写出![]() 的数量关系.
的数量关系.
【答案】(1)(0,4)或(0,-4);(2)![]() ;(3)答案见解析
;(3)答案见解析
【解析】(1)先根据S△ABM =S□ABDC,得出△ABM的高为4,再根据三角形面积公式得到M点的坐标;
(2)先计算出S梯形OBDC=5,再讨论:当点P运动到点B时,S△POC的最小值=2,当点P运动到点D时,S△POC的最大值=3,即可判断S=S△PCD+S△POB的取值范围的取值范围;
(3)分类讨论:当点P在BD上,如图1,作PE∥CD,根据平行线的性质得CD∥PE∥AB,则∠DCP=∠EPC,∠BOP=∠EPO,易得∠DCP+∠BOP=∠EPC+∠EPO=∠CPO;
当点P在线段BD的延长线上时,如图2,同样有∠DCP=∠EPC,∠BOP=∠EPO,由于∠EPO-∠EPC=∠BOP-∠DCP,于是∠BOP-∠DCP=∠CPO;同理可得当点P在线段DB的延长线上时,∠DCP-∠BOP=∠CPO.
解:(1)由题意,得C(0,2)
∴□ABDC的高为2
若S△ABM =S□ABDC,则△ABM的高为4
又∵点M是y轴上一点
∴点M的坐标为(0,4)或(0,-4)
(2)∵B(-2,0),O(0,0)
∴OB=2
由题意,得C(0,2),D(-3,2)
∴OC=2,CD=3
∴S梯形OBDC=![]()
点![]() 在线段
在线段![]() 上运动,
上运动,
当点![]() 运动到端点B时,△PCO的面积最小,为
运动到端点B时,△PCO的面积最小,为![]()
当点![]() 运动到端点D时,△PCO的面积最大,为
运动到端点D时,△PCO的面积最大,为![]()
∴S=S△PCD+S△POB= S梯形OBDC-S△PCO=5-S△PCO
∴S的最大值为5-2=3,最小值为5-3=2
故S的取值范围是:![]()
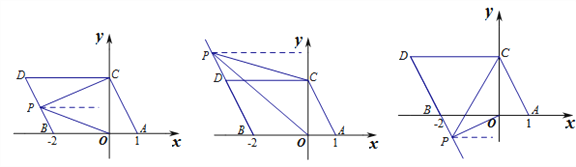
(3)如图:
当点![]() 在线段
在线段![]() 上运动时,
上运动时,![]()
当点![]() 在射线
在射线![]() 上运动时,
上运动时,![]()
当点![]() 在射线
在射线![]() 上运动时,
上运动时,![]()

 阅读快车系列答案
阅读快车系列答案