Question

【题目】(12分)

(1) 填空：

(a－b)(a＋b)＝________；

(a－b)(a2＋ab＋b2)＝________；

(a－b)(a3＋a2b＋ab2＋b3)＝________．

(2) 猜想：

(a－b)(an－1＋an－2b＋…＋abn－2＋bn－1)＝________ (其中n为正整数，且n≥2)．

(3) 利用(2)猜想的结论计算： 29－28＋27－…＋23－22＋2

Answer 1

【答案】（1）a2﹣b2，a3﹣b3，a4﹣b4；（2）an﹣bn；（3）342

【解析】试题分析：（1）根据平方差公式与多项式乘以多项式的运算法则运算即可；

（2）根据（1）的规律可得结果；

（3）原式变形后，利用（2）得出的规律计算即可得到结果．

试题解析：（1）（a-b）（a+b）=a2-b2；

（a-b）（a2+ab+b2）=a3+a2b+ab2-a2b-ab2-b3=a3-b3；

（a-b）（a3+a2b+ab2+b3）=a4+a3b+a2b2+ab3-a3b-a2b2-ab3-b4=a4-b4；

（2）由（1）的规律可得：

原式=an-bn，

（3）29-28+27-…+23-22+2=（2-1）（28+26+24+22+2）=342．

法二：29-28+27-…+23-22+2

=29-28+27-…+23-22+2-1+1

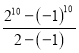=+1

=342.