题目内容
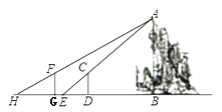
【题目】某水库大坝的横截面是如图所示的四边形BACD,期中AB∥CD.瞭望台PC正前方水面上有两艘渔船M、N,观察员在瞭望台顶端P处观测渔船M的俯角![]() ,观测渔船N在俯角
,观测渔船N在俯角![]() ,已知NM所在直线与PC所在直线垂直,垂足为点E,PE长为30米.
,已知NM所在直线与PC所在直线垂直,垂足为点E,PE长为30米.
(1)求两渔船M,N之间的距离(结果精确到1米);
(2)已知坝高24米,坝长100米,背水坡AD的坡度![]() .为提高大坝防洪能力,某施工队在大坝的背水坡填筑土石方加固,加固后坝定加宽3米,背水坡FH的坡度为
.为提高大坝防洪能力,某施工队在大坝的背水坡填筑土石方加固,加固后坝定加宽3米,背水坡FH的坡度为![]() ,施工12天后,为尽快完成加固任务,施工队增加了机械设备,工作效率提高到原来的1.5倍,结果比原计划提前20天完成加固任务,施工队原计划平均每天填筑土石方多少立方米?(参考数据:
,施工12天后,为尽快完成加固任务,施工队增加了机械设备,工作效率提高到原来的1.5倍,结果比原计划提前20天完成加固任务,施工队原计划平均每天填筑土石方多少立方米?(参考数据: ![]() )
)

【答案】20m;600立方米.
【解析】试题(1)根据已知求出EN,根据正切的概念求出EM,求差得到答案;
(2)根据坡度和锐角三角函数的概念求出截面积和土石方数,根据题意列出分式方程,解方程得到答案.
试题解析:(1)在Rt△PEN中,∵∠PNE=45°,
∴EN=PE=30米,
在Rt△PEM中,∠PME=31°,tan∠PME=![]() ,
,
∴ME=![]() ≈50(米),
≈50(米),
∴MN=EM-EN=20米,
答:两渔船M,N之间的距离约为20米;
(2)过点F作FK∥AD交AH于点K,过点F作FL⊥AH交直线AH于点L,
则四边形DFKA为平行四边形,

∴∠FKA=∠DAB,DF=AK=3,
由题意得,tan∠FKA=tan∠DAB=4,tan∠H=![]() ,
,
在Rt△FLH中,LH=![]() =36,
=36,
在Rt△FLK中,KL=![]() =6,
=6,
∴HK=30,AH=33,
梯形DAHF的面积为: ![]() ×DL×(DF+AH)=432,
×DL×(DF+AH)=432,
所以需填土石方为432×100=43200,
设原计划平均每天填x立方米,由题意得,
12x+(![]() -12-20)×1.5x=43200,
-12-20)×1.5x=43200,
解得,x=600,
经检验x=600是方程的解.
答:原计划平均每天填筑土石方600立方米.

【题目】已知二次函数y=ax2+bx+c的y与x的部分对应值如下表:
x | -1 | 0 | 1 | 3 |
y | -3 | 1 | 3 | 1 |
下列结论:①抛物线的开口向下;②其图象的对称轴为x=1;③当x<1时,函数值y随x的增大而增大;④方程ax2+bx+c=0有一个根大于4,其中正确的结论有( )
A. 1个 B. 2个 C. 3个 D. 4个
【题目】某通信公司策划了![]() 两种上网的月收费方式:
两种上网的月收费方式:
收费方式 | 月使用费/元 | 包时上网时间/ | 超时费/(元/ |
| 30 | 25 | 0.05 |
|
|
|
|
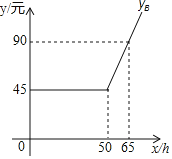
设每月上网时间为![]() ,方式
,方式![]() 的收费金额分别为
的收费金额分别为![]() (元),
(元),![]() (元),如图是
(元),如图是![]() 与
与![]() 之间函数关系的图象.(友情提示:若累计上网时间不超出包时上网时间,则只收月使用费;若累计上网时间超出包时上网时间,则对超出部分再加收超时费)
之间函数关系的图象.(友情提示:若累计上网时间不超出包时上网时间,则只收月使用费;若累计上网时间超出包时上网时间,则对超出部分再加收超时费)
(1)![]() ,
,![]() ,
,![]() ;
;
(2)求![]() 之间的函数解析式;
之间的函数解析式;
(3)若每月上网时间为31小时,请直接写出选择哪种方式能节省上网费.