��Ŀ����
����Ŀ��ij��վ����A��B�������������շѷ�ʽ��
�շѷ�ʽ | ��ʹ�÷�/Ԫ | ��ʱ����ʱ��/h | ��ʱ��/��Ԫ/min�� |
A | 30 | 25 | 0.05 |
B | m | n | P |
��ÿ������ѧϰʱ��Ϊx��h��Сʱ������A��B���շѽ��ֱ�ΪyA ��Ԫ����yB��Ԫ����
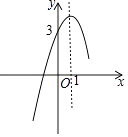
��ͼ��yB��x֮�亯����ϵ��ͼ��
��������ʾ�����ۼ�����ʱ�䲻��������ʱ����ʱ�䡱����ֻ�ա���ʹ�÷ѡ������ۼ�����ʱ�䲻��������ʱ����ʱ�䡱����Գ��������ټ��ա���ʱ�ѡ���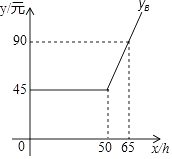
��1��m=��n=p= ��
��2��д��yA��x֮��ĺ�����ϵʽ��
��3����ÿ��������ʱ��Ϊ29Сʱ����˵��ѡȡ���ַ�ʽ�ܽ�ʡ�����ѣ�
���𰸡�
��1��45,50,0.05
��2���⣺��0��x��25ʱ��yA=30��
��x��25ʱ��yA=30+0.05��60��x��25��=3x��45��
���Ͽɵã�yA= ![]()
��3���⣺��x=29ʱ��
yA=3��29��45=33��
yB=45��
��yA��yB��
����ÿ��������ʱ��Ϊ29Сʱ��ѡ��A�ַ�ʽ�ܽ�ʡ������
���������⣺��1���ɺ���ͼ��ɵã�
m=45��n=50��p=��90��45���£�65��50����60=0.05��
���Դ��ǣ�45��50��0.05��

��ϰ��ϵ�д�
�����Ŀ