��Ŀ����
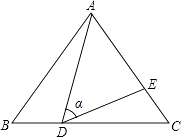
����Ŀ������֪,��ABCD�С�ABC=90��,AB=4cm��BC=8cm,AC�Ĵ�ֱƽ����EF�ֱ�AD��BC�ڵ�E��F,����ΪO.
(1)��ͼ1������AF��CE.��֤: �ı���AFCEΪ����.
(2)��ͼ1����AF�ij�.
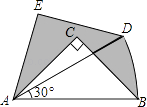
(3)��ͼ2������P��Q�ֱ��A��C����ͬʱ����,�ء�AFB�͡�CDE���������˶�һ��.����P��A��F��B��Aֹͣ,��Q��C��D��E��Cֹͣ.���˶�������, ��P���ٶ�Ϊÿ��1cm����Q���ٶ�Ϊÿ��0.8cm,���˶�ʱ��Ϊ�룬����A��P��C��Q�ĵ�Ϊ������ı�����ƽ���ı���ʱ,��t��ֵ.



���𰸡�(1)������;(2)5cm;(3) ![]() ��.
��.
����������1������ȫ���Ƴ�OE=OF���ó�ƽ���ı���AFCE�����������ж��Ƴ����ɣ�
��2�������������ʵó�AF=CF�����ݹ��ɶ����ó����̣�������̵Ľ⼴����
��3����������ۿ�֪����P����BF�ϡ�Q����ED��ʱ�����ܹ���ƽ���ı��Σ�����ƽ���ı��ε������г�������⼴�ɣ�
��1��֤�������ı���ABCD��ƽ���ı��Σ�
��AD��BC��
���CAD=��ACB����AEF=��CFE��
��EF��ֱƽ��AC������ΪO��
��OA=OC��
���AOE�ա�COF��
��OE=OF��
���ı���AFCEΪƽ���ı���
��AC��EF
���ı���![]() Ϊ����
����
��2����EF��ֱƽ��AC
��AF=CF
����AF=CF=xcm����BF=��8��x��cm��
��Rt��ABF�У�AB=4cm���ɹ��ɶ�����![]() ��
��
���x=5����AF=5cm��
��3���� ��Ȼ��P����AF��ʱ��Q����CD�ϣ���ʱA��C��P��Q�ĵ㲻���ܹ���ƽ���ı��Σ�
ͬ��P����AB��ʱ��Q����DE��CE�ϣ�Ҳ���ܹ���ƽ���ı��Σ�
���ֻ�е�P����BF�ϡ�Q����ED��ʱ�����ܹ���ƽ���ı��Σ�
����A��C��P��Q�ĵ�Ϊ������ı�����ƽ���ı���ʱ��PC=QA��
�ߵ�P���ٶ�Ϊÿ��1cm����Q���ٶ�Ϊÿ��0.8cm���˶�ʱ��Ϊt�룬
��PC=t��QA=12��0.8t����t=12��0.8t�����![]() ��
��
����A��C��P��Q�ĵ�Ϊ������ı�����ƽ���ı���ʱ![]() ��
��

����Ŀ��������������ˮƽ����ߣ������������������Խ��Խ�࣮��Щ���������ȴ��Ϊ��ͨ��ȫ��һ�������������������ijУ��ѧ��ȤС���ڡ��������������ĵ��鱨�桷�о͡�����Ϊ���������������Ч�Ĺ�����ʩ�������ij�������־���������ʾ����飬���е����ʾ���������ѡ�ֻѡһ���
A����ǿ��ͨ����ѧϰ��
B��ʵ�����չ�����
C���Ӵ�ͨΥ���������ȣ�
D�����������������
E����ʱ���·������
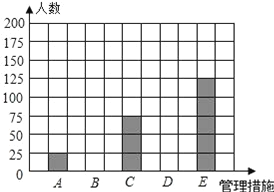
�������ݵIJ���ͳ�ƽ�����±���
������ʩ | �ش����� | �ٷֱ� |
A | 25 | 5% |
B | 100 | m |
C | 75 | 15% |
D | n | 35% |
E | 125 | 25% |
�ϼ� | a | 100% |
��1����������ͳ�Ʊ��е����ݿɵ�m=_____��n=_____��a=_____��
��2���ڴ���У���ȫ����ͳ��ͼ��
��3���������о���2600�ˣ������������������������ѡ��D������������������ľ���Լ�ж����ˣ�