题目内容
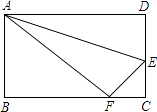
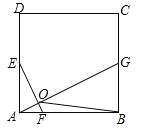
【题目】如图,在正方形ABCD中,点E、G分别是边AD、BC的中点,AF=![]() AB.
AB.
(1)求证:EF⊥AG;
(2)若点F、G分别在射线AB、BC上同时向右、向上运动,点G运动速度是点F运动速度的2倍,EF⊥AG是否成立(只写结果,不需说明理由)?
(3)正方形ABCD的边长为4,P是正方形ABCD内一点,当![]() ,求△PAB周长的最小值.
,求△PAB周长的最小值.
【答案】(1)证明见解析;(2)成立;(3)![]() .
.
【解析】
试题分析:(1)由正方形的性质得出AD=AB,∠EAF=∠ABG=90°,证出![]() ,得出△AEF∽△BAG,由相似三角形的性质得出∠AEF=∠BAG,再由角的互余关系和三角形内角和定理证出∠AOE=90°即可;
,得出△AEF∽△BAG,由相似三角形的性质得出∠AEF=∠BAG,再由角的互余关系和三角形内角和定理证出∠AOE=90°即可;
(2)证明△AEF∽△BAG,得出∠AEF=∠BAG,再由角的互余关系和三角形内角和定理即可得出结论;
(3)过O作MN∥AB,交AD于M,BC于N,则MN⊥AD,MN=AB=4,由三角形面积关系得出点P在线段MN上,当P为MN的中点时,△PAB的周长最小,此时PA=PB,PM=![]() MN=2,连接EG,则EG∥AB,EG=AB=4,证明△AOF∽△GOE,得出
MN=2,连接EG,则EG∥AB,EG=AB=4,证明△AOF∽△GOE,得出![]() =
=![]() ,证出
,证出![]() =
=![]() ,得出AM=
,得出AM=![]() AE=
AE=![]() ,由勾股定理求出PA,即可得出答案.
,由勾股定理求出PA,即可得出答案.
试题解析:(1)证明:∵四边形ABCD是正方形,∴AD=AB,∠EAF=∠ABG=90°,∵点E、G分别是边AD、BC的中点,AF=![]() AB,∴
AB,∴![]() =
=![]() ,
,![]() =
=![]() ,∴
,∴![]() ,∴△AEF∽△BAG,∴∠AEF=∠BAG,∵∠BAG+∠EAO=90°,∴∠AEF+∠EAO=90°,∴∠AOE=90°,∴EF⊥AG;
,∴△AEF∽△BAG,∴∠AEF=∠BAG,∵∠BAG+∠EAO=90°,∴∠AEF+∠EAO=90°,∴∠AOE=90°,∴EF⊥AG;
(2)解:成立;理由如下:
根据题意得:![]() =
=![]() ,∵
,∵![]() =
=![]() ,∴
,∴![]() =
=![]() ,又∵∠EAF=∠ABG,∴△AEF∽△BAG,∴∠AEF=∠BAG,∵∠BAG+∠EAO=90°,∴∠AEF+∠EAO=90°,∴∠AOE=90°,∴EF⊥AG;
,又∵∠EAF=∠ABG,∴△AEF∽△BAG,∴∠AEF=∠BAG,∵∠BAG+∠EAO=90°,∴∠AEF+∠EAO=90°,∴∠AOE=90°,∴EF⊥AG;
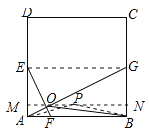
(3)解:过O作MN∥AB,交AD于M,BC于N,如图所示:
则MN⊥AD,MN=AB=4,∵P是正方形ABCD内一点,当S△PAB=S△OAB,∴点P在线段MN上,当P为MN的中点时,△PAB的周长最小,此时PA=PB,PM=![]() MN=2,连接EG、PA、PB,则EG∥AB,EG=AB=4,∴△AOF∽△GOE,∴
MN=2,连接EG、PA、PB,则EG∥AB,EG=AB=4,∴△AOF∽△GOE,∴![]() =
=![]() ,∵MN∥AB,∴
,∵MN∥AB,∴![]() =
=![]() ,∴AM=
,∴AM=![]() AE=
AE=![]() ×2=
×2=![]() ,由勾股定理得:PA=
,由勾股定理得:PA=![]() =
=![]() ,∴△PAB周长的最小值=2PA+AB=
,∴△PAB周长的最小值=2PA+AB=![]() .
.

 名校联盟快乐课堂系列答案
名校联盟快乐课堂系列答案