Question

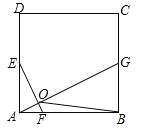
【题目】将一个直角三角形纸片放置在平面直角坐标系中，点，点，点.是边上的一点（点不与点重合），沿着折叠该纸片，得点的对应点.

（1）如图①，当点在第一象限，且满足时，求点的坐标；

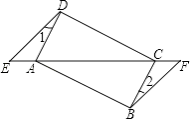
（2）如图②，当为中点时，求的长；

（3）当时，求点的坐标（直接写出结果即可）.

Answer 1

【答案】（1）点A’的坐标为（，1）；（2）1；（3）或 .

【解析】

试题分析：（1）因点，点，可得OA= ,OB=1，根据折叠的性质可得△A’OP≌△AOP，由全等三角形的性质可得OA’=OA=,在Rt△A’OB中，根据勾股定理求得的长，即可求得点A的坐标；（2）在Rt△AOB中，根据勾股定理求得AB=2，再证△BOP是等边三角形，从而得∠OPA =120°.在判定四边形OPA’B是平行四边形，根据平行四边形的性质即可得的长；

试题解析：（1）因点，点，

∴OA= ,OB=1.

根据题意，由折叠的性质可得△A’OP≌△AOP.

∴OA’=OA=,

由，得∠A’BO=90°.

在Rt△A’OB中，,

∴点A’的坐标为（，1）.

(2) 在Rt△AOB中，OA= ,OB=1,

∴

∵当为中点，

∴AP=BP=1,OP=AB=1.

∴OP=OB=BP,

∴△BOP是等边三角形

∴∠BOP=∠BPO=60°，

∴∠OPA=180°-∠BPO=120°.

由（1）知，△A’OP≌△AOP，

∴∠OPA’=∠OPA=120°，P’A=PA=1，

又OB=PA’=1，

∴四边形OPA’B是平行四边形.

∴A’B=OP=1.

(3)或 .