Question

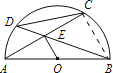
【题目】如图，以AB为直径的半圆O内有一条弦AC，点E是弦AC的中点，连接BE，并延长交半圆O于点D，若OB＝2，OE＝1，则∠CDE的度数是_______________.

Answer 1

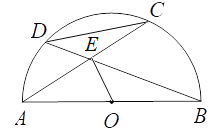
【答案】30°

【解析】

连接BC．构建∠CAB与∠CDE是所对的圆周角．根据三角形的中位线定理，求得△AEO是直角三角形，然后在直角三角形AEO中由30°角所对的直角边是斜边的一半，求得∠CAB=30°；最后根据圆周角定理求得∠CDE=30°

连接BC．

∵AB是直径，

∴∠ACB=90°；

∵E是弦AC的中点，O是直径AB的中点，

∴OE∥BC，

∴OE⊥AC；

∵OB=2，OE=1，

∴AO=2，

∴AO=2OE，

∴∠CAB=30°（30°角所对的直角边是斜边的一半）；

∴∠CDE=30°（同弧所对的圆周角相等）；

故答案是：30°．