题目内容
【题目】复习“全等三角形”的知识时,老师布置了一道作业题:
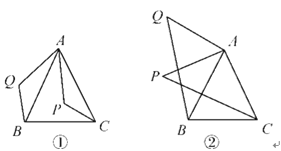
“如图①,已知,在△ABC中,AB=AC,P是△ABC内任意一点,将AP绕点A顺时针旋转至AQ,使∠QAP=∠BAC,连接BQ,CP,则BQ=CP.”
小亮是个爱动脑筋的同学,他通过对图①的分析,证明了△ABQ≌△ACP,从而证得BQ=CP之后,他将点P移到等腰三角形ABC外,原题中其他条件不变,发现“BQ=CP”仍然成立,请你就图②给出证明.
【答案】证明见解析.
【解析】
如图②,由∠QAP=∠BAC易得∠QAB=∠PAC,这样结合AB=AC,AQ=AP即可证得:△ABQ≌△ACP,从而可得BQ=CP.
∵∠QAP=∠BAC,
∴∠QAP+∠PAB=∠PAB+∠BAC,即∠QAB=∠PAC,
在△ABQ和△ACP中: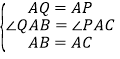 ,
,
∴△ABQ≌△ACP,
∴BQ=CP.

练习册系列答案
 ABC考王全优卷系列答案
ABC考王全优卷系列答案
相关题目