题目内容
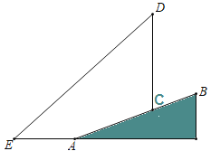
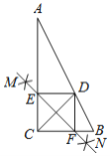
【题目】如图,Rt△ABC中,∠ACB=90°,CD平分∠ACB交AB于点D,按下列步骤作图:
步骤1:分别以点C和点D为圆心,大于![]() 的长为半径作弧,两弧相交于M,N两点;
的长为半径作弧,两弧相交于M,N两点;
步骤2:作直线MN,分别交AC,BC于点E,F;
步骤3:连接DE,DF.
若AC=4,BC=2,则线段DE的长为![]()
![]()
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
【答案】D
【解析】
先根据角平分线的性质得到∠ECD=∠DCF=45°,再根据垂直平分线的性质得到CE=DE,∠ECD=∠EDC=45°,进而得到∠CED=90°,证得DE∥CB,所以△AED∽△ACB,设ED=x,根据相似三角形对应线段成比例列式求出x即可.
∵CD平分∠ACB,∴∠ECD=∠DCF=45°,∵MN垂直平分CD,∴CE=DE,∴∠ECD=∠EDC=45°,∴∠CED=90°,又∵∠ACB=90°,∴DE∥CB,∴△AED∽△ACB,![]() ,设ED=x,则EC=x,AE=4-x,∴
,设ED=x,则EC=x,AE=4-x,∴![]() ,解得x=
,解得x=![]() ,故选D.
,故选D.

练习册系列答案
相关题目