题目内容
【题目】如图,矩形![]() 的两条边
的两条边![]() 的长是方程
的长是方程![]() 的两根
的两根![]() 沿直线
沿直线![]() 将矩形折叠,点
将矩形折叠,点![]() 落在第一象限的点
落在第一象限的点![]() 处,
处,![]() 交
交![]() 轴于点
轴于点![]() .
.
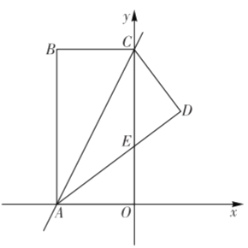
(1)求点![]() 和点
和点![]() 的坐标;
的坐标;
(2)将直线![]() 以每秒
以每秒![]() 个单位长度的速度沿
个单位长度的速度沿![]() 轴向下平移,求直线
轴向下平移,求直线![]() 扫过的三角形
扫过的三角形![]() 的面积
的面积![]() 关于运动的时间
关于运动的时间![]() 的函数关系式;
的函数关系式;
(3)在(2)的条件下,在移动的直线![]() 上是否存在点
上是否存在点![]() ,使以为
,使以为![]() 顶点的四边形是平行四边形?若存在,请直接写出点
顶点的四边形是平行四边形?若存在,请直接写出点![]() 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
【答案】(1)![]() ;(2)
;(2)![]() ;(3)存在,
;(3)存在,![]()
【解析】
(1)由一元二次方程可先求得OA、OC的长,则可求得A、B的坐标;设![]() ,根据折叠的性质以及矩形的性质得AE=CE,在
,根据折叠的性质以及矩形的性质得AE=CE,在![]() 中根据勾股定理可求出a的值,从而可解决问题;
中根据勾股定理可求出a的值,从而可解决问题;
(2)由FG//AC可得![]() ,根据相似三角形面积比等于相似比的平方可得出S与t之间的函数关系式;
,根据相似三角形面积比等于相似比的平方可得出S与t之间的函数关系式;
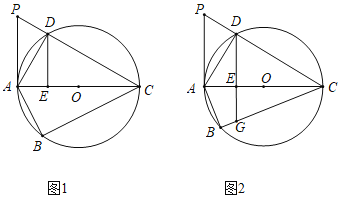
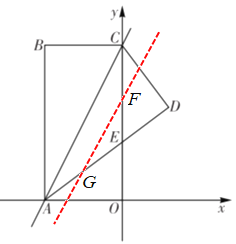
(3)分两种情况求解:①过点D作DN//y轴,交x轴于点N,交移动后的直线AC于点M,
连接OM,假定EOMD是平行四边形,求出OM的长,通过解直角三角形OMN,求出ON和MN的长度即可;②方法同①.
![]() 解方程
解方程![]()
得![]()
![]()
![]()
![]()
设![]() ,则
,则![]()
由折叠可得![]()
![]()
![]()
![]()
![]()
在![]() 中,
中,![]()
解得![]() ,
,![]()
![]()
![]() 设直线
设直线![]() 平移
平移![]() 秒时,交
秒时,交![]() 于点
于点![]() ,
,
则![]()
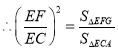
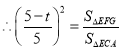
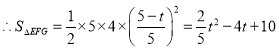
![]()
![]() 存在
存在
分两种情况:①如图,过点D作DN//y轴,交x轴于点N,交移动后的直线AC于点M,
连接OM,
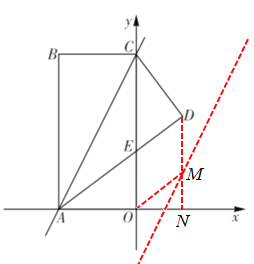
∵OE=3,OA=4,
∴tan∠OAE=![]() ,
,
设DN=3x,则AN=4x,
由折叠的性质可得AD=AB=8,
在Rt△AND中,由勾股定理可得,![]()
解得,![]()
∴![]() ,
,![]() ,
,
∴![]()
假设四边形EOMD是平行四边形,则有OM//ED,
∴∠MON=∠DAN
∴![]() ,
,
∴![]()
∴M点的坐标为(![]() ,
,![]() ) ;
) ;
②如图,过点O作OM//AD,交移动后的直线AC于点M,连接OD,ME,过M作MN⊥x轴,垂足为点N,
由(1)得AE=5,AD=8,
∴DE=3,
假设四边形EMOD是平行四边形,则有OM=ED=3,
同①可得![]()
设MN=3x,则ON=4x,
在Rt△OMN中,由勾股定理可得,![]()
解得,![]()
∴![]() ,
,![]() ,
,
∴M点的坐标为(![]() ,
,![]() ) .
) .
综上,M点的坐标为(![]() ,
,![]() )或(
)或(![]() ,
,![]() ).
).

【题目】“赏中华诗词,寻文化基因,品生活之美”,某校举办了首届“中国诗词大会”,经选拔后有![]() 名学生参加决赛,这
名学生参加决赛,这![]() 名学生同时默写
名学生同时默写![]() 首古诗词,若每正确默写出一首古诗词得
首古诗词,若每正确默写出一首古诗词得![]() 分,根据测试成绩绘制出部分频数分布表和部分频数分布直方图如下:
分,根据测试成绩绘制出部分频数分布表和部分频数分布直方图如下:
组别 | 成绩 | 频数(人数) |
第 |
|
|
第 |
|
|
第 |
|
|
第 |
|
|
第 |
|
|
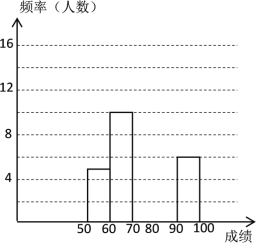
请结合图表完成下列各题: :
(1)①求表中![]() 的值;
的值;
②频数分布直方图补充完整;
(2)若测试成绩不低于![]() 分为优秀,则本次测试的优秀率是多少?
分为优秀,则本次测试的优秀率是多少?
(3)第![]() 组
组![]() 名同学中,有
名同学中,有![]() 名男同学,现将这
名男同学,现将这![]() 名同学平均分成两组进行对抗赛,且
名同学平均分成两组进行对抗赛,且![]() 名男同学每组分两人,求其中小华和小强两名男同学能分在同一组的概率.
名男同学每组分两人,求其中小华和小强两名男同学能分在同一组的概率.