题目内容
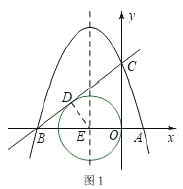
【题目】如图1,已知抛物线![]() (
(![]() )与
)与![]() 轴交于
轴交于![]() 、
、![]() 两点(
两点(![]() 在
在![]() 的右侧),与
的右侧),与![]() 轴的正半轴交于点
轴的正半轴交于点![]() ,对称轴与
,对称轴与![]() 轴交于点
轴交于点![]() ,作直线
,作直线![]() .
.
(1)求点![]() 、
、![]() 、
、![]() 的坐标:
的坐标:
(2)当以![]() 为圆心的圆与
为圆心的圆与![]() 轴和直线
轴和直线![]() 都相切时,求抛物线的解析式:
都相切时,求抛物线的解析式:
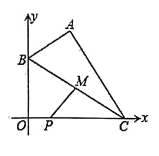
(3)在(2)的条件下,如图2.![]() 是
是![]() 轴负半轴上的一点,过点
轴负半轴上的一点,过点![]() 作
作![]() 轴的平行线,与直线
轴的平行线,与直线![]() 交于点
交于点![]() ,与抛物线交于点
,与抛物线交于点![]() ,连接
,连接![]() ,将
,将![]() 沿
沿![]() 翻折,
翻折,![]() 的对应点为
的对应点为![]() .在图2中探究:是否存在点
.在图2中探究:是否存在点![]() ,使得
,使得![]() 恰好落在
恰好落在![]() 轴上?若存在,请求出
轴上?若存在,请求出![]() 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.

【答案】(1)![]() ,
,![]() ,
,![]()
![]() ;(2)
;(2)![]() ;(3)存在,点
;(3)存在,点![]() 坐标为
坐标为![]() 或
或![]()
【解析】
(1)根据对称轴x=![]() 可求得抛物线对称轴,得点E的坐标,令y=0即可求出点A、B的坐标;
可求得抛物线对称轴,得点E的坐标,令y=0即可求出点A、B的坐标;
(2)由圆的切线性质得DE⊥BC,运用勾股定理可求BD=2,再根据解三角形知识即可建立关于a的方程,求出a的值;
(3)由翻折得∠MCN=∠M′CN证得,![]() 作MF⊥y轴于F,根据
作MF⊥y轴于F,根据![]() ,转化得到关于t的方程,即可求得点P的坐标.
,转化得到关于t的方程,即可求得点P的坐标.
(1)∵对称轴为![]() ,
,
∴点![]() 的坐标为
的坐标为![]() .
.
令![]() ,得
,得![]() ,
,
∴![]() ,
,![]() ,
,
∴![]() ,
,![]() ;
;
(2)如图1中,设![]() 与直线
与直线![]() 相切于点
相切于点![]() ,连接
,连接![]() ,则
,则![]() ,
,
∵![]() ,
,![]() ,
,![]() ,
,
∴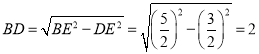 ,
,
∵![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴抛物线解析式为![]() ;
;
(3)如图2中,由折叠可得![]() , .
, .
∵![]() 轴,
轴,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
由抛物线解析式为![]() ,令x=0,得y=3
,令x=0,得y=3
∴C(0,3)
设直线BC解析式为y=kx+b,
由题意得![]() ,解得
,解得![]() ,
,
∴直线![]() 解析式为
解析式为![]() ,
,
设![]() ,
,![]() ,
,
作![]() 于
于![]() ,,
,,
∵![]() ,
,
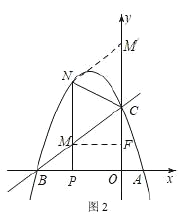
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
解得:![]() (舍),
(舍),![]() ,
,![]() .
.
∴满足条件的点![]() 坐标为
坐标为![]() 或
或![]() .
.

【题目】某班“数学兴趣小组”对函数![]() ,的图象和性质进行了探究过程如下,请补充完成:
,的图象和性质进行了探究过程如下,请补充完成:
(1)函数![]() 的自变量
的自变量![]() 的取值范围是__________________;
的取值范围是__________________;
(2)下表是![]() 与
与![]() 的几组对应值.请直接写出
的几组对应值.请直接写出![]() ,
,![]() 的值:
的值:![]() ______________;
______________;![]() ________.
________.
| … |
|
| 0 |
|
|
|
| 2 | 3 | 4 | … |
| … |
|
|
|
| -3 | 5 | 3 |
|
| … |
(3)如图,在平面直角坐标系![]() 中,描出了以上表中各对对应值为坐标的点,根据描出的点,画出该函数的图象;
中,描出了以上表中各对对应值为坐标的点,根据描出的点,画出该函数的图象;
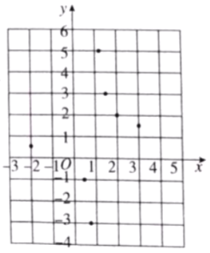
(4)通过观察函数的图象,小明发现该函数图象与反比例函数![]() 的图象形状相同,是中心对称图形,且点
的图象形状相同,是中心对称图形,且点![]() 和
和![]() 是一组对称点,则其对称中心的坐标为________.
是一组对称点,则其对称中心的坐标为________.
(5)请写出一条该函数的性质:___________________.
(6)当![]() 时,关于
时,关于![]() 的方程
的方程![]() 有实数解,求
有实数解,求![]() 的取值范围.
的取值范围.