题目内容
【题目】我们知道:三角形的三条角平分线交于一点,这个点称为三角形的内心(三角形内切圆的圆心).现在规定:如果四边形的四个角的角平分线交于一点,我们把这个点也成为“四边形的内心”.
(1)试举出一个有内心的四边形.
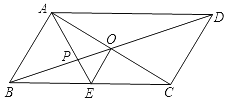
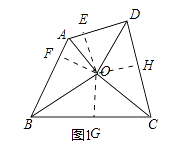
(2)如图1,已知点O是四边形ABCD的内心,求证:AB+CD=AD+BC.
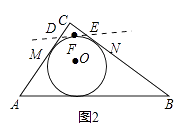
(3)如图2,Rt△ABC中,∠C=90°.O是△ABC的内心.若直线DE截边AC,BC于点D,E,且O仍然是四边形ABED的内心.这样的直线DE可画多少条?请在图2中画出一条符合条件的直线DE,并简单说明作法.
(4)问题(3)中,若AC=3,BC=4,满足条件的一条直线DE∥AB,求DE的长.
【答案】
(1)解:菱形
(2)解:作OE⊥AD与E,OF⊥AB与F,CG⊥BC与G,OH⊥CD与H,
∵∠AEO=∠AFO=90°
∴O是四边形ABCD的内心
∴∠EAO=∠FAO
在Rt△AEO和Rt△AFO中,
![]()
∴Rt△AEO≌Rt△AFO(HL)
∴AE=AF,
同理:BF=BG,CG=CH,DH=DE,
∴AE+DEBG+CG=AF+BF+CH+DH
即:AD+BC=AB+CD
(3)解:有无数条
作△ABC的内切圆圆O,切AC,BC于M、N,在弧MN上取一点F,作过F点作圆O的切线,交AB于E,交AC于D,沿DE剪裁,
(4)解:作CG⊥AB与点G,

由勾股定理得:AB= ![]()
∴ ![]() =2.4
=2.4
设△ABC的内切圆的半径为r,则r= ![]() =1
=1
∵DE∥AB
∴△CDE∽△CAB
∴ ![]() ∴
∴ ![]()
∴ ![]()
【解析】(1)根据四边形的每一条对角线平分一组对角,即可得答案。
(2)根据内心是各个角的平分线的交点,过交点O分别作四边的垂线段,根据角平分线的性质及全等三角形的判定和性质,可证得结果。
(3)可画无数条。
(4)根据勾股定理求得AB的长,根据面积相等求出CG的长,由三角形的内切圆半径和三角形三边关系式可求出r的长。根据相似三角形的性质,建立方程,求出DE的长。
【考点精析】关于本题考查的勾股定理的概念和三角形的内切圆与内心,需要了解直角三角形两直角边a、b的平方和等于斜边c的平方,即;a2+b2=c2;三角形的内切圆的圆心是三角形的三条内角平分线的交点,它叫做三角形的内心才能得出正确答案.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案【题目】抗震救灾中,某县粮食局为了保证库存粮食的安全,决定将甲、乙两个仓库的粮食,全部转移到具有较强抗震功能的A、B两仓库.已知甲库有粮食100吨,乙库有粮食80吨,而A库的容量为70吨,B库的容量为110吨.从甲、乙两库到A、B两库的路程和运费如下表:(表中“元/吨千米”表示每吨粮食运送1千米所需人民币)
路程(千米) | 运费(元/吨千米) | |||
甲库 | 乙库 | 甲库 | 乙库 | |
A库 | 20 | 15 | 12 | 12 |
B库 | 25 | 20 | 10 | 8 |
(1)若甲库运往A库粮食x吨,请写出将粮食运往A、B两库的总运费y(元)与x(吨)的函数关系式;
(2)当甲、乙两库各运往A、B两库多少吨粮食时,总运费最省,最省的总运费是多少?
【题目】我市某中学举行十佳歌手大赛,高、初中部根据初赛成绩,各选出5名选手组成初中代表队和高中代表队参加学校决赛.两个队各选出的5名选手的决赛成绩如图所示.
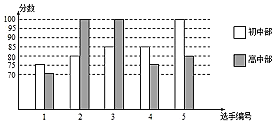
(1)根据所给信息填空:
平均数(分) | 中位数(分) | 众数(分) | 方差 | |
初中部 | 85 | ______ | 85 | _______ |
高中部 | _____ | 80 | ______ | 160 |
(2)你觉得高中部和初中部的决赛成绩哪个更好?说明理由.