题目内容
【题目】在矩形![]() 内放置正方形甲、正方形乙、等腰直角三角形丙,它们的摆放位置如图所示,已知
内放置正方形甲、正方形乙、等腰直角三角形丙,它们的摆放位置如图所示,已知![]() ,图中阴影部分的面积之和为31,则矩形
,图中阴影部分的面积之和为31,则矩形![]() 的周长为___________.
的周长为___________.

【答案】![]()
【解析】
设甲正方形的边长为a,乙正方形的边长为b,结合图形特征及隐含的关系式,用含a,b的代数式表示出有关线段,再利用![]() 建立方程,得到a=
建立方程,得到a=![]() ,再统一用b表示出各个部分的面积,运用阴影部分的面积之和为31建立方程解得b的值,从而求得矩形的周长.
,再统一用b表示出各个部分的面积,运用阴影部分的面积之和为31建立方程解得b的值,从而求得矩形的周长.
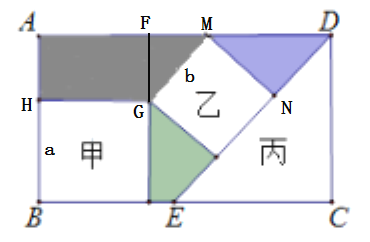
解:设甲正方形的边长为a,乙正方形的边长为b,则HB=HG=AF=a,GM=MN=b,
如图过点G作GF⊥AD,则![]() 为等腰直角三角形
为等腰直角三角形
∴FG=FM=AH=![]() GM=
GM=![]() b,MD=
b,MD=![]() MN=
MN=![]() b,
b,
∴AB=BH+AH=a+![]() b,BC=AD=AF+FM+MD=a+
b,BC=AD=AF+FM+MD=a+![]() b+
b+![]() b=a+
b=a+![]() b,
b,
∵AB:BC=5:9,
∴( a+![]() b) :(a+
b) :(a+![]() b)=5 :9,
b)=5 :9,
解得:a=![]() ,
,
∴CD=AB= a+![]() b=
b=![]() +
+![]() b=
b=![]() ,BC=
,BC=![]()
∴![]() ,
,![]() ,
,![]() ,
,
∵![]() ,
,
而 ![]()
![]() =
=![]() ,
,
![]() ,
,
∵![]() =31,
=31,
∴![]() =16
=16
∴b=4
∴矩形![]() 的周长为2(AB+BC)=2(
的周长为2(AB+BC)=2(![]() )=
)=![]()
故答案为:![]() .
.

练习册系列答案
相关题目