题目内容

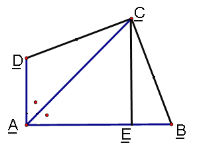
【题目】如图，将矩形纸片ABCD（如图①）按如下步骤操作：（1）以过点A的直线为折痕折叠纸片，使点B恰好落在AD边上，折痕与BC边交于点E（如图②）；（2）以过点E的直线为折痕折叠纸片，使点A落在BC边上，折痕EF交AD边于点F（如图③）；（3）将纸片展平，那么∠AFE的度数为_________.

【答案】67.5°

【解析】

先根据图形的翻折变换的性质得出∠BAE=∠AEB=45°，再根据平行线的性质得出∠DFA的度数，进而可得出∠AEF的度数.

因为AB=BE，∠ABE=90°，所以∠AEB=∠BAE=45°，在图（3）中，因为DF∥CE，所以∠DFA=∠EAF=45°，由图形翻折变换的性质可以知道∠AFE=，即∠AFE=67.5°.

练习册系列答案
相关题目

【题目】如图，在平面直角坐标系中，一次函数y =ax+b的图像与反比例函数y =的图像交于A（4，﹣2）、B（﹣2，m）两点，与x轴交于点C.

（1）求a，m的值；

（2）请直接写出不等式ax+b≥的解集；

（3）点P在反比例函数图像上，且点P的横坐标为－4，在平面直角坐标系中是否存在一点Q，使得以A、B、P、Q为顶点的四边形为平行四边形？如果存在，请直接写出点Q的坐标.

【题目】如图，在平面直角坐标系中，点A，B的坐标分别为(－1，0)，(3，0)，现同时将A，B两点向右平移1个单位，再向上平移2个单位，分别得到点A，B的对应点C，D，连接AC，BD，CD.

(1)求点C，D的坐标；

(2)若点P在直线BD上运动，连接PC，PO.

①若点P在线段BD上(不与B，D重合)时，求S△CDP＋S△BOP的取值范围；

②若点P在直线BD上运动，试探索∠CPO，∠DCP，∠BOP的关系，并证明你的结论．

【题目】某校八年级共有800名学生，准备调查他们对“低碳”知识的了解程度．

（1）在确定调查方式时，团委设计了以下三种方案：

方案一：调查八年级部分女生；

方案二：调查八年级部分男生；

方案三：到八年级每个班去随机调查一定数量的学生．

请问其中最具有代表性的一个方案是_____；

（2）团委采用了最具有代表性的调查方案，并用收集到的数据绘制出两幅不完整的统计图（如图①、图②所示），请你根据图中信息，将两个统计图补充完整；

（3）请你估计该校八年级约有多少名学生比较了解“低碳”知识．

【题目】在一个不透明的布袋里装有4个标有1，2，3，4的小球，它们的形状、大小完全相同，小明从布袋里随机取出一个小球，记下数字为x，小红在剩下的3个小球中随机取出一个小球，记下数字为y

（1）计算由x、y确定的点（x，y）在函数y=﹣x+5的图象上的概率．

（2）小明和小红约定做一个游戏，其规则为：若x、y满足xy＞6，则小明胜；若x、y满足xy＜6，则小红胜，这个游戏公平吗？请说明理由；若不公平，请写出公平的游戏规则．

【题目】已知：AC平分∠BAD，CE⊥AB，∠B+∠D=180°，求证：AE=AD+BE

【题目】如图，在一个单位为1的方格纸上，△A1A2A3，△A3A4A5，△A5A6A7，…，是斜边在x轴上、斜边长分别为2，4，6，…的等腰直角三角形．若△A1A2A3的顶点坐标分别为A1(2，0)，A2(1，-1)，A3(0，0)，则依图中所示规律，A2017的横坐标为（ ）

A. 1010 B. 2 C. 1 D. ﹣1006

【题目】我们已经知道(a﹣b)2≥0，即a2﹣2ab+b2≥0．所以a2+b2≥2ab(当且仅当a=b时取等号)．

阅读1：若a、b为实数，且a＞0，b＞0．

∵()2≥0，∴a﹣2+b≥0，∴a+b≥2(当且仅当a=b时取等号)．

阅读2：若函数y=x(m＞0，x＞0，m为常数)．由阅读1结论可知：x即x∴当x即x2=m，∴x=(m＞0)时，函数y=x的最小值为2．

阅读理解上述内容，解答下列问题：

问题1：当x＞0时，的最小值为　　　　；当x＜0时，的最大值为　　　　．

问题2：函数y=a+(a＞1)的最小值为　　　　．

问题3：求代数式(m＞﹣2)的最小值，并求出此时的m的值．

问题4：如图，四边形ABCD的对角线AC，BD相交于点O，△AOB、△COD的面积分别为4和16，求四边形ABCD面积的最小值．

【题目】如图，点D为⊙O上一点，点C在直径BA的延长线上，且∠CDA=∠CBD．（1）判断直线CD和⊙O的位置关系，并说明理由．

（2）过点B作⊙O的切线BE交直线CD于点E，若AC=2，⊙O的半径是3，求∠BEC的正切值．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网