��Ŀ����
����Ŀ����ͼ����PΪ������y=![]() x2��һ���㣮
x2��һ���㣮
��1����������y=![]() x2����������y=
x2����������y=![]() ��x+2��2��1ͨ��ͼ��ƽ�Ƶõ��ģ���д��ƽ�ƵĹ��̣�
��x+2��2��1ͨ��ͼ��ƽ�Ƶõ��ģ���д��ƽ�ƵĹ��̣�
��2����ֱ��l����y����һ��N����ƽ����x�ᣬ��N������Ϊ��0����1��������P��PM��l��M��
������̽������ͼһ���ڶԳ������Ƿ����һ����F��ʹ��PM=PF������������ڣ������F�����꣺�������ڣ���˵�����ɣ�
������������ͼ��������Q������Ϊ��1.5������QP+PF����Сֵ��

���𰸡���1������ƽ��1����λ��������2����λ����2������0��1������5
����������1���ҵ������߶������꼴���ҵ�ƽ�Ʒ�ʽ��
��2���������P���꣬����PM=PF����BF�����F���ꣻ
������PM=PF����QP+PFת��ΪQP+QM�����ô��߶���̽�����⣮
��1����������![]() �Ķ���Ϊ����2����1��
�Ķ���Ϊ����2����1��
��������![]() ��ͼ������ƽ��1����λ��������2����λ�õ�������
��ͼ������ƽ��1����λ��������2����λ�õ�������![]() ��ͼ��
��ͼ��
��2���ٴ���һ����F��ʹ��PM=PF�������
��ͼһ������P��PB��y���ڵ�B
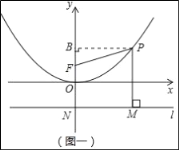
���P����Ϊ![]() ,
,
��![]() ,
,
��![]()
��![]() ��
��
![]()
��OF=1
���F������0��1��
���ɢ���PM=PF��
![]() ����СֵΪ
����СֵΪ![]() ����Сֵ
����Сֵ
��Q��P��M���㹲��ʱ��QP+QM����СֵΪ��Q������5��
��QP+PF����СֵΪ5��

 �߽�������ϵ�д�
�߽�������ϵ�д�