题目内容
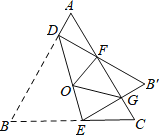
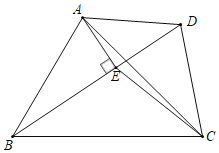
【题目】如图,在四边形ABCD中,tan∠ABC=![]() ,BD为对角线,∠ABD+∠BDC=90°,过点A作AE⊥BD于点E,连接CE,若AE=
,BD为对角线,∠ABD+∠BDC=90°,过点A作AE⊥BD于点E,连接CE,若AE=![]() DE,EC=DC=5,则△ABC的面积为_____.
DE,EC=DC=5,则△ABC的面积为_____.
【答案】![]() .
.
【解析】
延长CE交AB于点H,延长DC、AE相交于点K,根据垂直的定义可得∠AEB=∠AED=90°,又∠ABD+∠BDC=90°,设∠ABD=α,用α的代数式分别表示出∠BDC、∠BAE、∠CED、∠CDE、∠AEH,由sinK=sin∠ABD求出AB的值,设CH=7a,BH=6a,分别用a的代数式表示出HE、AH,再根据tan∠AEH=tan∠ABE可得EH2=AHBH,据此得出a的值,进而得出CH的值,再根据三角形的面积公式即可得出△ABC的面积.
如图,延长CE交AB于点H,延长DC、AE相交于点K,
∵AE⊥BD,
∴∠AEB=∠AED=90°,
∵∠ABD+∠BDC=90°,
设∠ABD=α,则∠BDC=90°﹣α,
∴∠BAE=90°﹣∠ABE=90°﹣α,
∵EC=DC,
∴∠CED=∠CDE=90°﹣α,
∵∠AEH=∠KEC=∠DEK﹣∠CED=α,
∴∠BHE=∠BAE +∠AEH =90°,
∵∠K+∠KDE=90°,∠CED+∠CEK=90°,∠KDE=∠CED,
∴∠K=∠CEK=α,
∴CK=CE=CD=5,即:DK=10,
∴sinK=sin∠ABD,即![]() ,
,
∴![]() ,
,
解得:![]() ,
,
∵,tan∠ABC=![]() ,
,
∴设CH=7a,BH=6a,
∴HE=HC﹣CE=7a﹣5,AH=AB﹣BH=![]() ,
,
∵∠AEH=∠ABE=α,
∴tan∠AEH=tan∠ABE,
∴EH2=AHBH,即(7a﹣5)2=(![]() )6a
)6a
解得:![]() (舍去),
(舍去),
∴CH=7a=7,
∴![]() .
.
故答案为:![]() .
.


练习册系列答案
 开心蛙口算题卡系列答案
开心蛙口算题卡系列答案
相关题目