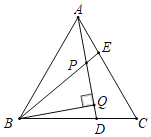
题目内容
【题目】请在下面括号里补充完整证明过程:
已知:如图,△ABC中,∠ACB=90°,AF平分∠CAB,交CD于点E,交CB于点F,且∠CEF=∠CFE.求证:CD⊥AB.

证明:∵AF平分∠CAB (已知)
∴ ∠1=∠2( )
∵∠CEF=∠CFE , 又∠3=∠CEF (对顶角相等)
∴∠CFE=∠3(等量代换)
∵在△ACF中,∠ACF=90°(已知)
∴( )+∠CFE=90°( )
∵∠1=∠2, ∠CFE=∠3(已证) ∴( )+( )=90°(等量代换)
在△AED中, ∠ADE=90°( 三角形内角和定理)
∴ CD⊥AB( ).
【答案】角平分线的定义;∠CAF;直角三角形中两锐角互余;∠2;∠3;垂直的定义
【解析】
首先根据角平分线定义可得∠1=∠2,然后再利用等量代换可得∠CFE=∠3,根据直角三角形中两锐角互余,得到∠CAF+∠CFE=90°,进而可得∠2+∠3=90°,再根据三角形内角和定理得∠ADE=90°,进而得到CD⊥AB.
证明:∵AF平分∠CAB (已知)
∴ ∠1=∠2(角平分线的定义)
∵∠CEF=∠CFE , 又∠3=∠CEF (对顶角相等)
∴∠CFE=∠3(等量代换)
∵在△ACF中,∠ACF=90°(已知)
∴∠CAF+∠CFE=90°(直角三角形中两锐角互余)
∵∠1=∠2, ∠CFE=∠3(已证) ∴(∠2)+(∠3)=90°(等量代换)
在△AED中, ∠ADE=90°(三角形内角和定理)
∴ CD⊥AB(垂直的定义).
故答案为:角平分线的定义;∠CAF;直角三角形中两锐角互余;∠2;∠3;垂直的定义.

练习册系列答案
相关题目