题目内容
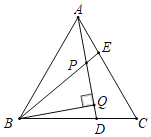
【题目】如图,△ABC为等边三角形,点D,E分别在BC,AC边上,且AE=CD,
AD,BE相交于点P.
(1)求证:△ABE≌△CAD.
(2)求∠BPD的度数.
(3)若BQ⊥AD于Q,PQ=3,PE=1,求AD的长.
【答案】(1)证明见解析;(2)60°;(3)7.
【解析】
(1)由SAS证明△ABE≌△CAD即可;
(2)由三角形全等可以得出∠ABE=∠CAD,由外角与内角的关系就可以得出答案.
(3)由全等三角形的性质得出BE=AD,求出∠BPQ=30°,由直角三角形的性质求出BP的长,即可求得BE的长,即可解题.
(1)证明:∵△ABC为等边三角形,
∴AB=BC=AC,∠ABC=∠ACB=∠BAC=60°.
在△ABE和△CAD中,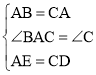 ,
,
∴△ABE≌△CAD(SAS);
(2)解:由(1)得:△ABE≌△CAD,
∴∠ABE=∠CAD.
∵∠BAD+∠CAD=60°,
∴∠BAD+∠ABE=60°.
∴∠BPD=∠ABE+∠BAD=60°.
(3)解:∵△ABE≌△CAD,
∴BE=AD,
∵BQ⊥AD,
∴∠PBQ=90°﹣∠BPD=30°,
∴BP=2PQ=6,
∴AD=BE=BP+PE=6+1=7.

【题目】甲、乙两校参加区教育局举办的学生英语口语竞赛,两校参赛人数相等.比赛结束后,发现学生成绩分别为7分、8分、9分、10分(满分为10分).依据统计数据绘制了如图所示的尚不完整的统计图表.
甲校成绩统计表
分数 | 7分 | 8分 | 9分 | 10分 |
人数 | 11 | 0 | 8 |

(1)在图①中,“7分”所在扇形的圆心角等于______![]() ;
;
(2)请你将②的统计图补充完整;
(3)经计算,乙校的平均分是8.3分,中位数是8分,请写出甲校的平均分、中位数;并从平均分和中位数的角度分析哪个学校成绩较好;
(4)如果该教育局要组织8人的代表队参加市级团体赛,为便于管理,决定从这两所学校中的一所挑选参赛选手,请你分析,应选哪所学校?




