题目内容
【题目】如图,![]() 的内接四边形
的内接四边形![]() 中
中![]() 为
为![]() 直径,
直径,![]() ,
,![]() 是
是![]() 的切线,
的切线,![]() 交
交![]() 的延长线于点
的延长线于点![]() .
.
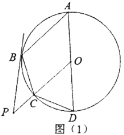
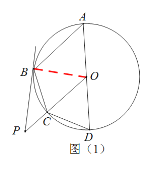
(1)如图(1)求证:![]() ;
;
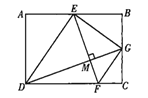
(2)如图(2)点![]() 在弧
在弧![]() 上,连接
上,连接![]() 分别交
分别交![]() 、
、![]() 于点
于点![]() 、
、![]() ,且
,且![]() ,求证:
,求证:![]() ;
;
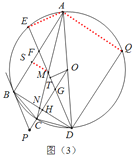
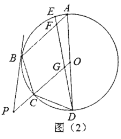
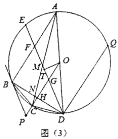
(3)如图(3)在(2)的条件下,连接![]() 分别交
分别交![]() 、
、![]() 于点
于点![]() 、
、![]() ,
,![]() ,垂足为
,垂足为![]() ,
,![]() 是
是![]() 上一点,连接
上一点,连接![]() ,已知
,已知![]() ,
,![]() ,
,![]() ,求
,求![]() 的长.
的长.
【答案】(1)证明见解析;(2)证明见解析;(3)DQ=14.
【解析】
(1)连接OB,根据切线性质∠CBP+∠OBC=90°,由OB=OC,结合三角形内角和易证∠BOC=2∠CBP,再由平行线性质可得∠BOC=∠ABO,∠COD=∠OAB,而∠OBA=∠OAB,所以∠COD=2∠CBP;
(2)由OC // AB可知∠AFE=∠DGC,将∠ADC+2∠.AFE=180°转化为∠OCD+2∠CGD=180°,即可得∠GCD=∠CDG,由等角对等边即可得到结论;
(3)连接AE、AQ,过M点作MS⊥AB于S,根据2∠ANB-∠ADQ=2∠ADB,可得四边形ABDQ为矩形,即DQ=AB,根据角的等量关系解三角形可知EF=![]() ,AE=
,AE=![]() ,设TM=|
,设TM=|![]() x,则DT=ET=4
x,则DT=ET=4![]() + x
+ x![]() ,DG=3
,DG=3![]() +
+ ![]() x,用三角函数可导出CD=CG=4+2x,GH=1+x, CD=3x+3,即4+2x=3x+3, 可得GH=4,BF=8,AF=6,即AB=DQ=14.
x,用三角函数可导出CD=CG=4+2x,GH=1+x, CD=3x+3,即4+2x=3x+3, 可得GH=4,BF=8,AF=6,即AB=DQ=14.
(1)连接OB,
∵BP是⊙O的切线,
∴OB⊥PB,
∵∠PBO=90,
∴∠CBP+∠OBC=90°,
∴2∠CBP+2∠OBC=180°,
∵OB=OC,
∴∠OBC=∠OCB,
∵∠OBC+∠OCB+∠BOC=180°,
∴2∠OBC+∠BOC=180°,
∴∠BOC=2∠CBP,
∵OC∥AB,
∴∠BOC=∠ABO,∠COD=∠OAB,
∵OB=OA,
∴∠OBA=∠OAB,
∴∠COD=2∠CBP.
(2)∵OC∥AB,
∴∠AFE=∠OGF,
∵∠CGD=∠OGF,
∴∠AFE=∠DGC,
∵∠ADC+2∠AFE=180,
∵OD=OC∴∠GCD=∠ADC,
∴∠GCD+2∠AFE=180,
∵∠GCD+∠CDG+∠CGD=180°,
∴∠GCD=∠CDG,
∴CD=CG;

(3)连接AE、AQ,过M点作MS⊥AB于S.
∵AD为⊙O直径,
∴AE⊥DE,
∴∠AED=90,
∵OT⊥DE,
∴TE=TD,∠OTD=90,
∴OT=![]() ,
,
∵OC∥AB,
![]() ,
,
∵EF=2TG=2![]() ,
,
![]() ,
,
![]() ,
,
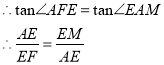
∵FM=![]() , 即EM=
, 即EM=![]() ,
,
∴AE=![]() ,
,
可得,tan∠EAF=![]() ,
,
解△AFM,可得tan∠FAM=![]() ,AF=6,
,AF=6,
设TM=![]() x,则
x,则![]()
用三角函数可导出CD=CG=![]() ,
,
∴CD=![]()
即![]()
解得![]()
∴GH=4,BF=8,AF=6
∴AB=14
∵∠ANB-∠ADB=∠CAD
又∵ 2∠ ANB-∠ADQ=2∠ADB,
∴∠ ADQ=2∠CAD,
由 (1) 可知∠BAD=2∠CAD,
∴∠ADQ= ∠BAD,
∴DQ∥AB∴四边形ABDQ的四角均为90°
∴四边形ABDQ为矩形,
∴DQ=AB=14