题目内容
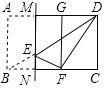
【题目】如图,在![]() 中,
中,![]() ,
,![]() ,以
,以![]() 为直径的
为直径的![]() 交
交![]() 于点
于点![]() ,连结
,连结![]() ,过点
,过点![]() 作
作![]() 交
交![]() 点
点![]() .连接
.连接![]() 交
交![]() 于点
于点![]() .
.
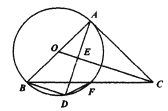
(1)求证:![]() .
.
(2)若![]() ,求
,求![]() 的值.
的值.
【答案】(1)证明见解析;(2)![]()
【解析】
(1)由AAS证明![]() 即可解答;(2)证明OE是△ABD的中位线,可得BD=2OE=2,(1)中全等得AE=BD=2,由勾股定理得
即可解答;(2)证明OE是△ABD的中位线,可得BD=2OE=2,(1)中全等得AE=BD=2,由勾股定理得![]() ,
,![]() ,又因为Rt△ABC是等腰直角三角形,BC=2
,又因为Rt△ABC是等腰直角三角形,BC=2![]() ,由三线合一得BF=FC=
,由三线合一得BF=FC=![]() BC=
BC=![]() ,因为在
,因为在![]() 中,
中,![]() ,所以设
,所以设![]() ,则
,则![]() ,
,![]() ,在Rt△BDH中,由勾股定理得:
,在Rt△BDH中,由勾股定理得:![]() ,解得
,解得![]() ,
,![]() (舍),再由勾股定理得
(舍),再由勾股定理得![]() .
.
(1)∵![]() 为直径,∴
为直径,∴![]() ,∴
,∴![]() ,
,
∵![]() ,∴
,∴![]() ,∴
,∴![]() .
.
∵![]() ,∴
,∴![]() ,∴
,∴![]() .
.
∵![]() ,∴
,∴![]() ,∴
,∴![]()
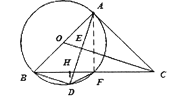
(2)连结![]() ,作
,作![]() ,则
,则![]() .
.
∵![]() ,
,![]() ,
,![]() ,∴
,∴![]() ,∴
,∴![]() ,AD=4.
,AD=4.
∴![]() ,
,![]() ,AC=
,AC=![]() ,
,
∵Rt△ABC是等腰直角三角形,BC=2![]() ,由三线合一得BF=FC=
,由三线合一得BF=FC=![]() BC=
BC=![]() ,
,
在![]() 中,
中,![]() ,
,
设![]() ,则
,则![]() ,
,![]() ,
,
∴在Rt△BDH中,由勾股定理得:![]() ,解得
,解得![]() ,
,![]() (舍),
(舍),
∴![]() ,(连结
,(连结![]() ,
,![]() ,证
,证![]() ,证等腰直角
,证等腰直角![]() 亦可)
亦可)

练习册系列答案
相关题目
【题目】发散思维2017·丰台区二模为了解某校八年级学生每周上网的时间,两名学生进行了抽样调查,小丽调查了八年级电脑爱好者中40名学生每周上网的时间,小杰从全校400名八年级学生中随机抽取了40名学生,调查了他们每周上网的时间.小丽与小杰整理各自的样本数据,如下表所示:
时间段(时/周) | 小丽抽样人数 | 小杰抽样人数 |
0~1 | 6 | 22 |
1~2 | 10 | 10 |
2~3 | 16 | 6 |
3~4 | 8 | 2 |
(表中每组数据包含最小值,不包含最大值)
(1)你认为哪名同学抽取的样本不合理?请说明理由;
(2)专家建议每周上网2小时以上(含2小时)的同学应适当减少上网的时间,估计该校全体八年级学生中有多少名学生应适当减少上网的时间.