题目内容
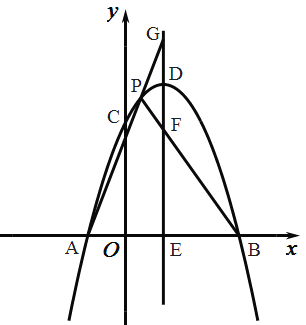
【题目】如图,一次函数y=k1x+b的图象与反比例函数y=![]() 的图象相交于A,B两点,点A的坐标为(﹣1,3),点B的坐标为(3,n).
的图象相交于A,B两点,点A的坐标为(﹣1,3),点B的坐标为(3,n).
(1)求这两个函数的表达式;
(2)点P在线段AB上,且S△APO:S△BOP=1:3,求点P的坐标.
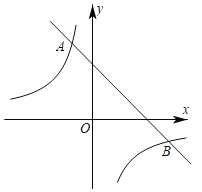
【答案】(1)反比例函数解析式为y=﹣![]() ;一次函数解析式为y=﹣x+2;(2)P点坐标为(0,2).
;一次函数解析式为y=﹣x+2;(2)P点坐标为(0,2).
【解析】
(1))先把点A点坐标代入y=![]() 中求出k2得到反比例函数解析式为y=-
中求出k2得到反比例函数解析式为y=-![]() ;再把B(3,n)代入y=-
;再把B(3,n)代入y=-![]() 中求出n得到得B(3,-1),然后利用待定系数法求一次函数解析式;
中求出n得到得B(3,-1),然后利用待定系数法求一次函数解析式;
(2)设P(x,-x+2),利用三角形面积公式得到AP:PB=1:3,即PB=3PA,根据两点间的距离公式得到(x-3)2+(-x+2+1)2=9[(x+1)2+(-x+2-3)2],然后解方程求出x即可得到P点坐标.
(1)把点A(﹣1,3)代入y=![]() 得k2=﹣1×3=﹣3,则反比例函数解析式为y=﹣
得k2=﹣1×3=﹣3,则反比例函数解析式为y=﹣![]() ;
;
把B(3,n)代入y=﹣![]() 得3n=﹣3,解得n=﹣1,则B(3,﹣1),
得3n=﹣3,解得n=﹣1,则B(3,﹣1),
把A(﹣1,3),B(3,﹣1)代入y=k1x+b得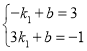 ,解得
,解得![]() ,
,
∴一次函数解析式为y=﹣x+2;
(2)设P(x,﹣x+2),
∵S△APO:S△BOP=1:3,
∴AP:PB=1:3,
即PB=3PA,
∴(x﹣3)2+(﹣x+2+1)2=9[(x+1)2+(﹣x+2﹣3)2],
解得x1=0,x2=﹣3(舍去),
∴P点坐标为(0,2).

练习册系列答案
 口算题卡北京妇女儿童出版社系列答案
口算题卡北京妇女儿童出版社系列答案
相关题目