题目内容
【题目】已知,抛物线y=ax2﹣4ax+2a(a≠0)
(1)求抛物线的对称轴;
(2)若抛物线经过点A(m,y1),B(n,y2),其中﹣4<m≤﹣3,2<n≤3,请依据a的取值情况直接写出y1与y2的大小关系;
(3)若矩形CDEF的顶点分别为C(1,2),D(1,﹣4),E(5,﹣4),F(5,2),若该抛物线与矩形的边有且只有两个公共点(包括矩形的顶点),求a的取值范围.
【答案】(1)x=2;(2)当a>0时,y1>y2;当a<0时,y1<y2;(3)a<﹣2或﹣1<a<0或0<a<2或a>4.
【解析】
(1)根据抛物线的对称轴公式求得即可;
(2)根据二次函数的图象和性质,根据抛物线的开口方向和增减性,判断点A、B离对称轴的远近,得出相应的函数值的大小关系,分为开口向上和开口向下两种情况进行分析解答;
(3)分两种情况,即a>0和a<0两种情况,根据抛物线的对称轴x=2,与x轴的交点(2﹣![]() ,0)和(2+
,0)和(2+![]() ,0),画出相应图形,分情况解答即可.
,0),画出相应图形,分情况解答即可.
解:(1)对称轴为x=﹣![]() =2,
=2,
答:抛物线的对称轴为直线x=2;
(2)抛物线y=ax2﹣4ax+2a=a(x﹣2)2﹣2a,
因此,抛物线的对称轴为x=2,顶点坐标为(2,﹣2a),
①当a>0时,抛物线开口向上,顶点在第四象限,
∵﹣4<m≤﹣3,2<n≤3,
∴根据横坐标离对称轴x=2的远近程度可得,y1>y2;
②当a<0时,抛物线开口向下,顶点在第一象限,
∵﹣4<m≤﹣3,2<n≤3,
∴根据横坐标离对称轴x=2的远近程度可得,y1<y2;
故有,当a>0时,y1>y2;当a<0时,y1<y2;
(3)当y=0时,即ax2﹣4ax+2a=0,
解得x1=2+![]() ,x2=2﹣
,x2=2﹣![]() ,
,
∴抛物线与x轴的交点坐标为A(2﹣![]() ,0),B(2+
,0),B(2+![]() ,0)
,0)
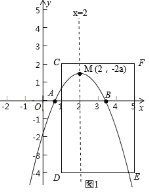
①当a<0时,如图1,顶点M(2,﹣2a)在第一象限,
Ⅰ)当顶点M在CD下方时,有0<﹣2a<2,解得﹣1<a<0,
Ⅱ)当顶点M在CD上方时,必须是抛物线左侧与CD的交点在点C的上方,
当抛物线过点C(1,2)时,a﹣4a+2a=2,解得,a=﹣2,此时M(2,4),
∴﹣2a>4,
解得a<﹣2;
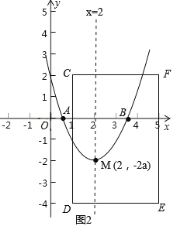
②当a>0时,如图2,顶点M(2,﹣2a)在第四象限,
Ⅰ)当顶点M在DE上方时,有﹣4<﹣2a<0,
解得0<a<2,
Ⅱ)当顶点M在DE下方时,必须是抛物线左侧与CD的交点在点D的下方,
当抛物线过点D(1,﹣4)时,a﹣4a+2a=﹣4,
解得a=4,此时M(2,﹣8),
∴﹣2a<﹣8,
解得a>4;
综上所述,当抛物线与矩形的边有且只有两个公共点(包括矩形的顶点)时,a的取值范围为a<﹣2或﹣1<a<0或0<a<2或a>4.

 阅读快车系列答案
阅读快车系列答案