题目内容
【题目】已知，如图所示的双曲线是函数
（m为常数，x＞0）图象的一支．
（1）求常数m的取值范围；
（2）若该函数的图象与一次函数y=x+1的图象在第一象限的交点为A（2，n），求点A的坐标及反比例函数的表达式．
【答案】（1）m＞3；（2）A (2，3)，y=
【解析】
（1）由反比例函数图象位于第一象限得到m-3大于0，即可求出m的范围；
（2）将A坐标代入一次函数解析式中求出n的值，确定出A坐标，代入反比例解析式中即可确定出反比例解析式．
解：（1）根据图象得m-3＞0，解得m＞3；
（2）∵点A（2，n）在一次函数y=x+1的图象上，
∴n=2+1=3，则A点的坐标为(2，3)．
又∵点A在反比例函数（m为常数，x＞0）的图象上，
∴m-3=2×3=6，
∴反比例函数的表达式为y=．
练习册系列答案
相关题目
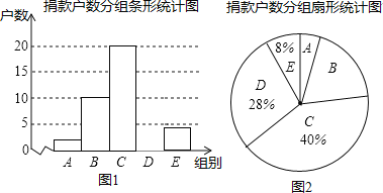
【题目】某社区组织“献爱心”捐款活动，并对部分捐款户数进行调查和分组统计，数据整理成如下统计图表（图中信息不完整）．
捐款户数分组统计表
组别 | 捐款额（x）元 | 户数 |
A | 1≤x＜100 | 2 |
B | 100≤x＜200 | 10 |
C | 200≤x＜300 | c |
D | 300≤x＜400 | d |
E | x≥400 | e |
请结合以上信息解答下列问题：
（1）本次调查的样本容量是______；
（2）d=______，并补全图1；
（3）图2中，“B”所对应扇形的圆心角为______度；
（4）若该社区有500户住户，根据以上信息估计全社区捐款不少于300元的户数是______．
