题目内容
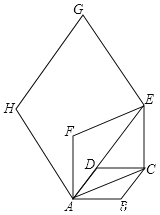
【题目】如图,在边长为1的菱形ABCD中,∠DAB=60°,连接对角线AC,以AC为边作第二个菱形ACC1D1,使∠D1AC=60°,连接AC1,再以AC1为边作第三个菱形AC1C2D2,使∠D2AC1=60°;…,按此规律所作的第六个菱形的边长为( )
A. 9 B. ![]() C. 27 D.
C. 27 D. ![]()
【答案】B
【解析】
先求出第一个菱形和第二个菱形的边长,得出规律,根据规律即可得出结论.
连接BD交AC于O,连接CD1交AC1于E,如图所示:
∵四边形ABCD是菱形,∠DAB=60°,
∴ACD⊥BD,∠BAO=![]() ∠DAB=30°,
∠DAB=30°,
OA=![]() AC,
AC,
∴OA=ABcos30°=1×![]() =
=![]() ,
,
∴AC=2OA=![]() ,
,
同理AE=ACcos30°=![]() ×
×![]() =
=![]() ,AC1=3=(
,AC1=3=(![]() )2,
)2,
…,
第n个菱形的边长为(![]() )n﹣1,
)n﹣1,
∴第六个菱形的边长为(![]() )5=9
)5=9![]() ,
,
故选B.

练习册系列答案
相关题目
【题目】为了解学生的体能情况,随机选取了1000名学生进行调查,并记录了他们对长跑、短跑、跳绳、跳远四个项目的喜欢情况,整理成以下统计表,其中“√”表示喜欢,“×”表示不喜欢.
项目 | 长跑 | 短跑 | 跳绳 | 跳远 |
200 | √ | × | √ | √ |
300 | × | √ | × | √ |
150 | √ | √ | √ | × |
200 | √ | × | √ | × |
150 | √ | × | × | × |
(1)估计学生同时喜欢短跑和跳绳的概率;
(2)估计学生在长跑、短跑、跳绳、跳远中同时喜欢三个项目的概率;
(3)如果学生喜欢长跑、则该同学同时喜欢短跑、跳绳、跳远中哪项的可能性大?